Diferencia entre el área y el perímetro
- 2075
- 177
- Maricarmen Moya
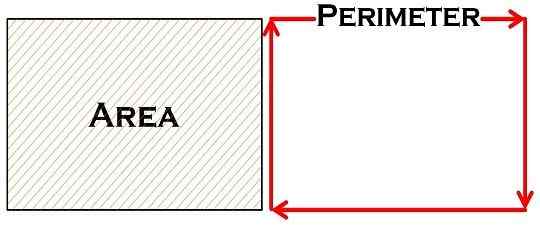
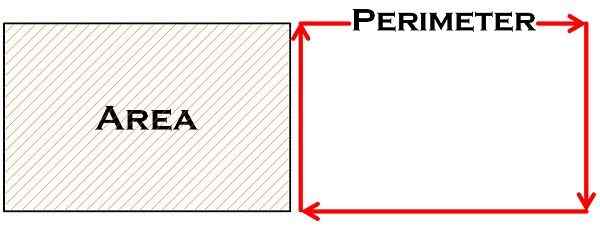Área y perímetro son dos conceptos fundamentales vitales de las matemáticas, que a menudo se entienden juntos. Estos dos conceptos se utilizan para medir el espacio físico de un objeto y forma una base para las matemáticas avanzadas. El perímetro a menudo se entiende como la longitud de la ruta que cubre una figura cerrada, mientras que el área se refiere al espacio cubierto por la figura cerrada.
Ambos conceptos tienen una aplicación práctica y se usan en nuestra vida cotidiana. Si bien el área no es más que el alcance de la superficie, el perímetro es la línea continua que forma un límite de una forma geométrica cerrada. Lea el artículo para conocer las diferencias básicas entre el área y el perímetro.
Contenido: área vs perímetro
- Cuadro comparativo
- Definición
- Diferencias clave
- Fórmulas
- Conclusión
Cuadro comparativo
| Base para la comparación | Área | Perímetro |
|---|---|---|
| Significado | El área se describe como la medición de la superficie del objeto. | El perímetro se refiere al contorno que rodea una figura cerrada. |
| Representa | Espacio ocupado por la figura. | Borde o límite de una figura. |
| Medición | Unidades cuadradas | Unidades lineales |
| Dimensiones involucradas | Dos | Uno |
| Ejemplo | Espacio cubierto por el jardín. | Longitud de la cerca requerida para encerrar el jardín. |
Definición de área
En matemáticas, el área de una superficie plana se define como la cantidad de espacio cubierto por él. Es una cantidad física que indica el número de unidades cuadradas ocupadas por el objeto bidimensional. Se usa para saber cuánto espacio se ocupa de una superficie plana. Se mide en unidades cuadradas, yo.mi. metros cuadrados, millas cuadradas, pulgadas cuadradas, etc.
El término área tiene un número final de uso práctico como en proyectos de construcción, agricultura, arquitectura, etc. Para medir el área de una superficie plana, debe contar la cantidad de cuadrados cubiertos por la forma.
Por ejemplo: Supongamos que necesita mosaico del piso de la habitación, la cantidad de mosaicos requeridos para cubrir toda la habitación será su área.
Definición de perímetro
El perímetro se define como una medida de la longitud del borde que rodea una figura geométrica cerrada. El término 'perímetro' se deriva de la palabra griega, 'peri' y 'medidor' que significa alrededor y medir. En geometría, implica la línea continua que forma la ruta fuera de la forma bidimensional.
En palabras simples, el perímetro no es más que la longitud del contorno de una figura. Para averiguar el perímetro de un objeto en particular, simplemente puede agregar la longitud de los lados, para llegar a su perímetro. El perímetro de un círculo se conoce comúnmente como su circunferencia.
Por ejemplo: a. Supongamos que envuelve una cuerda alrededor del cuadrado, la longitud de la cuerda sería su perímetro.
b. Caminas a las afueras del jardín, la distancia cubierta sería el perímetro del jardín.
Diferencias clave entre el área y el perímetro
Las diferencias significativas entre el área y el perímetro se proporcionan en detalle, en los siguientes puntos:
- El área se describe como la medición de la superficie del objeto. El perímetro se refiere al contorno que rodea una figura cerrada.
- .El área representa el espacio ocupado por el objeto. Por el contrario, el perímetro indica el borde exterior o el límite de la forma.
- La medición del área se realiza en unidades cuadradas i.mi. Kilómetros cuadrados, pies cuadrados, pulgadas cuadradas, etc. Por otro lado, el perímetro de una forma se mide en unidades lineales I.mi. kilómetros, pulgadas, pies, etc.
- Como el perímetro se mide en unidades lineales, solo mide una dimensión i.mi. Longitud del objeto. Mientras que, en el caso del área, están involucradas dos dimensiones I.mi. longitud y ancho del objeto.
Fórmulas
| Objeto | Área | Perímetro | Variable |
|---|---|---|---|
| Cuadrado | a^2 | 4A | donde, a = longitud del lado |
| Rectángulo | L × B | 2 (L+B) | donde, l = longitud B = amplitud |
| Círculo | πr^2 | 2πr = πd | donde, r = radio |
| Triángulo | 1/2 bh | A+B+C | donde, b = base H = altura a, b, c = longitud de los lados |
| Rombo | (PQ)/2 | 4A | donde, a = lado P y Q son diagonales |
| Paralelogramo | bh | 2 (A+B) | donde b = base H = altura a = lado |
| Trapecio | ½ (A+B) × H | A+B+C+D | donde a = base b = base H = altura c = lado d = lado |
Conclusión
Después de revisar los puntos anteriores, está bastante claro que estos dos conceptos matemáticos son diferentes, pero puede usar uno para descubrir otro. Mientras que el área simplemente significa, el 'espacio cubierto' i.mi. Dentro del objeto, el perímetro se refiere a la distancia de '.mi. el contorno de la forma. Además, las cifras con el mismo perímetro pueden tener un área diferente y las cifras con la misma área pueden tener un perímetro diferente.