Diferencia entre ASA y AAS

ASA vs AAS: ASA significa "ángulo, lado, ángulo", mientras que AAS significa "ángulo, ángulo, lado"

La geometría es divertida. La geometría se trata de formas, tamaños y dimensiones. La geometría es el tipo de matemáticas que se ocupa del estudio de las formas. Es fácil ver por qué la geometría tiene tantas aplicaciones relacionadas con la vida real. Se usa en todo: en ingeniería, arquitectura, arte, deportes y mucho más. Hoy discutiremos la geometría del triángulo, específicamente congruencia del triángulo. Pero primero, necesitamos entender lo que significa ser congruente. Dos cifras son congruentes si se puede trasladar al otro de tal manera que todas sus partes coincidan. En otras palabras, dos figuras se llaman congruentes si son la misma forma y tamaño. Dos figuras congruentes son la misma figura, en dos lugares diferentes.

Es cierto que la congruencia del triángulo es el bloque básico de la construcción para muchos conceptos y pruebas geométricas. El congruencia del triángulo es uno de los conceptos geométricos más comunes en los estudios de secundaria. Un concepto importante a menudo se pasa por alto en la enseñanza y el aprendizaje sobre la congruencia del triángulo es el concepto de suficiencia, es decir, determinar las condiciones que satisfacen que dos triángulos son congruentes. Hay cinco formas de determinar si dos triángulos son congruentes, pero vamos a discutir solo dos, es decir, ASA y AAS. ASA significa "ángulo, lado, ángulo", mientras que AAS significa "ángulo, ángulo, lado". Echemos un vistazo a cómo usar los dos para determinar si dos triángulos son congruentes.

¿Qué es la congruencia del triángulo asa??

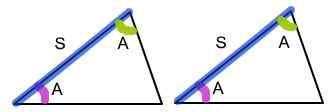
ASA significa "ángulo, lado, ángulo", lo que significa que dos triángulos son congruentes si tienen un lado igual contenido entre los ángulos iguales correspondientes. Si los vértices de dos triángulos están en correspondencia uno a uno, de modo que dos ángulos y el lado incluido de un triángulo son congruentes, respectivamente, a los dos ángulos y al lado incluido de los segundos triángulos, entonces satisface la condición de que la condición de la condición de que Los triángulos son congruentes. Debido a que los dos ángulos y el lado incluido son iguales en ambos triángulos, los triángulos se llaman congruentes.

¿Qué es la congruencia del triángulo de AAS??

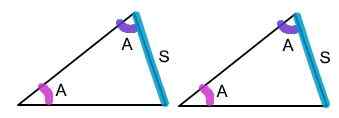
AAS significa "ángulo, ángulo, lado", lo que significa dos ángulos y un lado opuesto. AAS es una de las cinco formas de determinar si dos triángulos son congruentes. Afirma que si los vértices de dos triángulos están en correspondencia uno a uno, de modo que dos ángulos y el lado opuesto a uno de ellos en un triángulo son congruentes a los ángulos correspondientes y al lado no incluido del segundo triángulo, entonces, entonces Los triángulos son congruentes. El lado no incluido es el lado opuesto a cualquiera de los dos ángulos que se usan. En términos simples, si dos pares de ángulos correspondientes y los lados opuestos a ellos son iguales en ambos triángulos, los dos triángulos son congruentes.

Diferencia entre ASA y AAS

Terminología de ASA y AAS

- ASA y AAS son dos postulados que nos ayudan a determinar si dos triángulos son congruentes. ASA significa "ángulo, lado, ángulo", mientras que AAS significa "ángulo, ángulo, lado". Dos cifras son congruentes si tienen la misma forma y tamaño. En otras palabras, dos figuras congruentes son la misma figura, en dos lugares diferentes. Mientras que ambos son los términos de geometría utilizados en pruebas y se relacionan con la colocación de ángulos y lados, la diferencia radica en cuándo usarlas. ASA se refiere a dos ángulos y al lado incluido, mientras que AAS se refiere a los dos ángulos correspondientes y al lado no incluido.

Congruencia

- Según la congruencia de ASA, dos triángulos son congruentes si tienen un lado igual contenido entre los ángulos iguales correspondientes. En otras palabras, si dos ángulos y un lado incluido de un triángulo son iguales a los ángulos correspondientes y el lado incluido del segundo triángulo, entonces los dos triángulos se llaman congruentes, de acuerdo con la regla de ASA. La regla de AAS, por otro lado, afirma que si los vértices de dos triángulos están en correspondencia uno a uno de tal manera que dos ángulos y el lado opuestos a uno de ellos en un triángulo son iguales a los ángulos correspondientes y los no incluido el lado del segundo triángulo, entonces los triángulos son congruentes.

Representación

- La principal diferencia entre las dos reglas de congruencia es que el lado se incluye en el ASA Postulado, mientras que el lado no se incluye en el AAS Postulado.

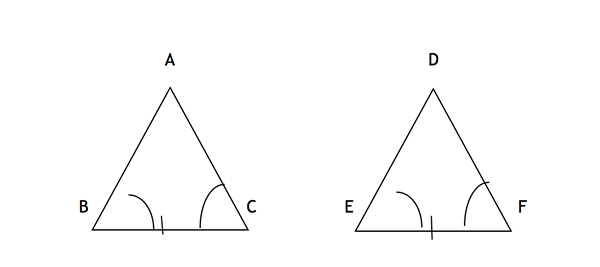
Aquí, dos ángulos (ABC y ACB) y el lado incluido (BC) son congruentes a los ángulos correspondientes (def y DFE) y un lado incluido (EF), lo que hace que los dos triángulos congruentes, según la regla de congruencia de ASA.

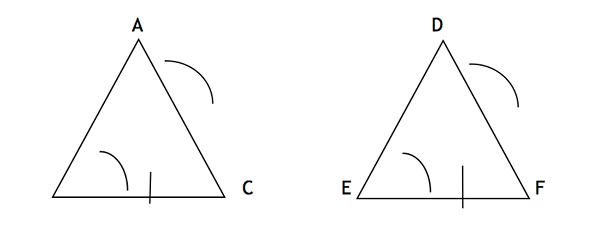
Aquí, dos ángulos (ABC y BAC) y un lado no incluido (BC) del primer triángulo son congruentes a los ángulos correspondientes (def y EDF) y el lado no incluido (EF) del segundo triángulo, lo que hace que el Dos triángulos congruentes. AC y EF también pueden ser los lados no incluidos de los dos triángulos respectivamente.

ASA VS. AAS: Gráfico de comparación

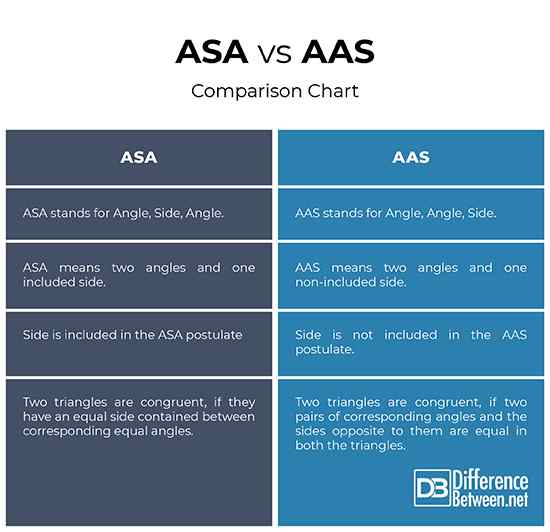
Resumen de ASA VS. Aas

En pocas palabras, ASA y AAS son dos de las cinco reglas de congruencia que determinan si dos triángulos son congruentes. ASA significa "ángulo, lado, ángulo", lo que significa que dos triángulos son congruentes si tienen un lado igual contenido entre los ángulos iguales correspondientes. AAS se refiere al "ángulo, ángulo, lado", lo que significa que si dos pares de ángulos correspondientes y los lados opuestos a ellos son iguales en ambos triángulos, los dos triángulos se llaman congruentes. Si bien ambos son básicamente la misma, la principal diferencia entre las dos reglas de congruencia es que el lado se incluye en la regla de ASA, mientras que el lado no está incluido en la regla de AAS.