Diferencia entre diferencial y derivado

Para comprender mejor la diferencia entre el diferencial y la derivada de una función, debe comprender primero el concepto de una función.

Una función es uno de los conceptos básicos en matemáticas que define una relación entre un conjunto de entradas y un conjunto de salidas posibles donde cada entrada está relacionada con una salida. Una variable es la variable independiente y la otra variable es la variable dependiente.

El concepto de función es uno de los temas más subestimados en matemáticas, pero es esencial para definir las relaciones físicas. Tomar, por ejemplo, la declaración "y es una función de x" significa que algo relacionado con y está directamente relacionado con x por alguna fórmula. Digamos si la entrada es 6 y la función es agregar 5 a la entrada 6. El resultado será 6+5 = 11, que es su salida.

Hay pocas excepciones en matemáticas o puede decir problemas, que no pueden resolverse mediante métodos ordinarios de geometría y álgebra solo. Se utiliza una nueva rama de las matemáticas conocida como cálculo para resolver estos problemas.

El cálculo es fundamentalmente diferente de las matemáticas que no solo usan las ideas de la geometría, la aritmética y el álgebra, sino que también se ocupan del cambio y el movimiento.

El cálculo como herramienta define la derivada de una función como el límite de un tipo particular. El concepto de derivada de una función distingue el cálculo de otras ramas de las matemáticas. El diferencial es un subcampo de cálculo que se refiere a la diferencia infinitesimal en una cantidad variable y es una de las dos divisiones fundamentales de cálculo. La otra rama se llama cálculo integral.

Que es diferencial?

El diferencial es una de las divisiones fundamentales del cálculo, junto con el cálculo integral. Es un subcampo de cálculo que se ocupa del cambio infinitesimal en una cantidad variable. El mundo en el que vivimos está lleno de cantidades interrelacionadas que cambian periódicamente.

Por ejemplo, el área de un cuerpo circular que cambia a medida que cambia el radio o un proyectil que cambia con la velocidad. Estas entidades cambiantes, en términos matemáticos, se denominan variables y la tasa de cambio de una variable con respecto a otra es un derivado. Y la ecuación que representa la relación entre estas variables se llama ecuación diferencial.

Las ecuaciones diferenciales son ecuaciones que contienen funciones desconocidas y algunas de sus derivadas.

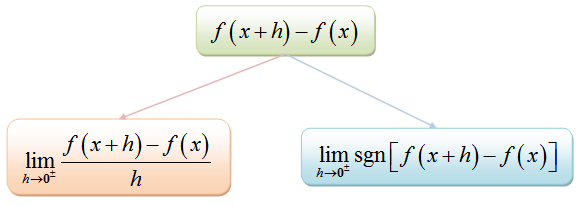
¿Qué es derivado??

El concepto de derivada de una función es uno de los conceptos más poderosos en matemáticas. La derivada de una función suele ser una nueva función que se denomina función derivada o función de velocidad.

La derivada de una función representa una tasa de cambio instantánea en el valor de una variable dependiente con respecto al cambio en el valor de la variable independiente. Es una herramienta fundamental del cálculo que también puede interpretarse como la pendiente de la línea tangente. Mide cuán empinado es el gráfico de una función en algún punto dado en el gráfico.

En términos simples, la derivada es la velocidad a la que la función cambia en algún punto particular.

Diferencia entre diferencial y derivado

Definición de diferencial VS. Derivado

Tanto los términos diferenciales como derivados están íntimamente conectados entre sí en términos de interrelación. En matemáticas, las entidades que cambian se denominan variables y la tasa de cambio de una variable con respecto a otra se llama derivado.

Las ecuaciones que definen la relación entre estas variables y sus derivadas se denominan ecuaciones diferenciales. La diferenciación es el proceso de encontrar un derivado. La derivada de una función es la tasa de cambio del valor de salida con respecto a su valor de entrada, mientras que el diferencial es el cambio real de función.

Relación de diferencial vs. Derivado

La diferenciación es un método para calcular una derivada que es la tasa de cambio de la salida y de la función con respecto al cambio de la variable x.

En términos simples, la derivada se refiere a la tasa de cambio de y con respecto a x, y esta relación se expresa como y = f (x), lo que significa que Y es una función de X. La derivada de la función f (x) se define como la función cuyo valor genera la pendiente de f (x) donde se define y f (x) es diferenciable. Se refiere a la pendiente del gráfico en un punto dado.

Representación de diferencial vs. Derivado

Los diferenciales se representan como dX, dY, dt, y así sucesivamente, donde dx representa un pequeño cambio en x, dy representa un pequeño cambio en y, y dt es un pequeño cambio en t. Al comparar los cambios en las cantidades relacionadas donde y es la función de x, el diferencial dy se pueden escribir como:

dy = F^'(X) dX

La derivada de una función es la pendiente de la función en cualquier punto y se escribe como d/dX. Por ejemplo, la derivada de SIN (x) se puede escribir como:

d/dx sin (x) = sin (x)^' = cos (x)

Diferencial VS. Derivado: Gráfico de comparación

Resumen de diferencial vs. Derivado

En matemáticas, la tasa de cambio de una variable con respecto a otra variable se llama derivada y las ecuaciones que expresan relación entre estas variables y sus derivadas se denominan ecuaciones diferenciales. En pocas palabras, las ecuaciones de diferencios involucran derivados que de hecho especifican cómo una cantidad cambia con respecto a otra. Al resolver una ecuación diferencial, obtienes una fórmula para la cantidad que no contiene derivadas. El método para calcular una derivada se llama diferenciación. En términos simples, la derivada de una función es la tasa de cambio del valor de salida con respecto a su valor de entrada, mientras que el diferencial es el cambio real de función.