Diferencia entre FFT y DFT

Transformación rápida de Fourier (FFT) vs. Transformación discreta de Fourier (DFT)

La tecnología y la ciencia van de la mano. Y no hay mejor ejemplo de esto que el procesamiento de señal digital (DSP). El procesamiento de señal digital es el proceso para optimizar la precisión y la eficiencia de las comunicaciones digitales. Todo es datos, ya sean las imágenes de las sondas del espacio exterior o las vibraciones sísmicas y cualquier cosa intermedia. Para convertir estos datos en formato legible humano usando computadoras es el procesamiento de señales digitales. Es una de las tecnologías más poderosas que combina la teoría matemática y la implementación física. El estudio de DSP comenzó como un curso de posgrado en ingeniería eléctrica, pero con el tiempo, se ha convertido en un posible gamechanger en el campo de la ciencia e ingeniería. Baste decir que, sin DSP, los ingenieros y científicos pueden dejar de existir.

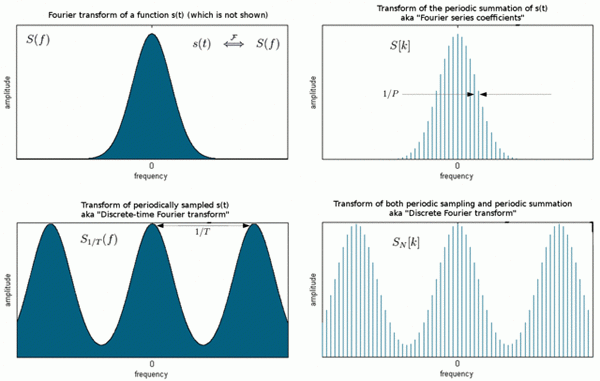
La transformación de Fourier es un medio para mapear una señal, en el dominio de tiempo o espacio en su espectro en el dominio de frecuencia. Los dominios de tiempo y frecuencia son solo formas alternativas de representar señales y la transformación de Fourier es la relación matemática entre las dos representaciones. Un cambio de señal en un dominio también afectaría la señal en el otro dominio, pero no necesariamente de la misma manera. La transformación discreta de Fourier (DFT) es una transformación como la transformación de Fourier utilizada con señales digitalizadas. Como su nombre indica, es la versión discreta del FT que ve el dominio de tiempo y el dominio de frecuencia como periódico. La transformación rápida de Fourier (FFT) es solo un algoritmo para el cálculo rápido y eficiente del DFT.

Transformación discreta de Fourier (DFT)

La transformación discreta de Fourier (DFT) es una de las herramientas más importantes en el procesamiento de señales digitales que calcula el espectro de una señal de duración finita. Es muy común codificar la información en los sinusoides que forman una señal. Sin embargo, en algunas aplicaciones, la forma de una forma de onda de dominio de tiempo no es una aplicación para señales en las que el contenido de frecuencia de señal de caso se vuelve muy útil en formas distintas de las señales digitales. La representación de una señal digital en términos de su componente de frecuencia en un dominio de frecuencia es importante. El algoritmo que transforma las señales de dominio de tiempo a los componentes del dominio de frecuencia se conoce como la transformación discreta de Fourier, o DFT.

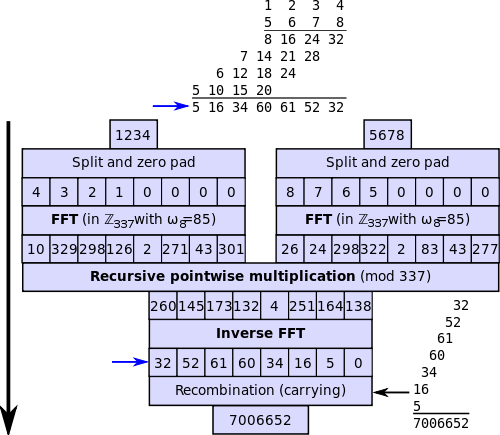
Transformación rápida de Fourier (FFT)

La transformación rápida de Fourier (FFT) es una implementación del DFT que produce casi los mismos resultados que el DFT, pero es increíblemente más eficiente y mucho más rápido lo que a menudo reduce el tiempo de cálculo significativamente. Es solo un algoritmo computacional utilizado para el cálculo rápido y eficiente del DFT. Varias técnicas rápidas de cálculo DFT conocidas colectivamente como la transformación rápida de Fourier, o FFT. Gauss fue el primero en proponer la técnica para calcular los coeficientes en una órbita trigonométrica de un asteroide en 1805. Sin embargo, no fue sino hasta 1965 que un artículo seminal de Cooley y Tukey llamó la atención de la comunidad de ciencias e ingeniería, que también sentó las bases de la disciplina del procesamiento de señales digitales.

Diferencia entre FFT y DFT

1. Significado de FFT y DFT

La transformación discreta de Fourier, o simplemente conocida como DFT, es el algoritmo que transforma las señales de dominio de tiempo en los componentes del dominio de frecuencia. DFT, como su nombre indica, es realmente discreto; Los conjuntos de datos de dominio de tiempo discretos se transforman en una representación de frecuencia discreta. En términos simples, establece una relación entre la representación del dominio del tiempo y la representación del dominio de la frecuencia. La transformación rápida de Fourier, o FFT, es un algoritmo computacional que reduce el tiempo de computación y la complejidad de grandes transformaciones. FFT es solo un algoritmo utilizado para el cálculo rápido del DFT.

2. Algoritmo de FFT y DFT

El algoritmo FFT más utilizado es el algoritmo Cooley-Tukey, que lleva el nombre de J. W. Cooley y John Tukey. Es un algoritmo de división y conquistar para el cálculo de la máquina de la serie compleja de Fourier. Rompe el DFT en DFT más pequeños. Otros algoritmos FFT incluyen el algoritmo de Rader, el algoritmo de transformación de Winograd Fourier, el algoritmo de transformación CHIRP Z, etc. Los algoritmos DFT se pueden programar en computadoras digitales de propósito general o implementarse directamente por hardware especial. El algoritmo FFT se usa para calcular el DFT de una secuencia o su inverso. Se puede realizar un DFT como o (n²) En la complejidad del tiempo, mientras que FFT reduce la complejidad del tiempo en el orden de O (NLogn).

3. Aplicaciones de FFT y DFT

El DFT se puede utilizar en muchos sistemas de procesamiento digital en una variedad de aplicaciones, como calcular el espectro de frecuencia de una señal, resolver aplicaciones diferenciales parciales, detección de objetivos de ecos de radar, análisis de correlación, calculación de multiplicación polinomial, análisis espectral y más. FFT se ha utilizado ampliamente para mediciones acústicas en iglesias y salas de conciertos. Otras aplicaciones de FFT incluyen análisis espectral en mediciones de video analógico, enteros grandes y multiplicación polinomial, algoritmos de filtrado, calcular distribuciones isotópicas, calcular coeficientes de series de Fourier, calcular convoluciones, generar ruido de baja frecuencia, diseñar kinormes, realizar matrices estructuradas en forma de ensayo, procesamiento de imágenes y procesamiento de imágenes y y y y y y y y y y y y y y y y y y más.

FFT vs. DFT: cuadro de comparación

Resumen de FFT vs. Dft

En pocas palabras, la transformación discreta de Fourier juega un papel clave en la física, ya que puede usarse como una herramienta matemática para describir la relación entre el dominio del tiempo y la representación del dominio de frecuencia de las señales discretas. Es un algoritmo simple pero bastante lento. Sin embargo, para reducir el tiempo informático y la complejidad de las transformaciones grandes, se puede usar un algoritmo más complejo pero menos lento como la transformación rápida de Fourier. FFT es una implementación del DFT utilizado para utilizado para el cálculo rápido del DFT. En resumen, FFT puede hacer todo lo que hace un DFT, pero de manera más eficiente y mucho más rápida que un DFT. Es una forma eficiente de calcular el DFT.