Diferencia entre la varianza de la muestra y la varianza de la población

Explicación

En estadísticas, el término muestreo se refiere a la selección de una parte de los datos estadísticos agregados con el fin de obtener información relevante sobre todo. El agregado o total de la información estadística sobre un carácter particular de todos los miembros cubiertos por la investigación se llama 'población' o 'universo'. (Das, N.GRAMO., 2010). La parte seleccionada de la población que se utiliza para obtener las características de la población o el universo se denomina 'muestra'. Se considera que la población está hecha de unidades o miembros individuales, y algunas de las unidades están incluidas en la muestra. El número total de unidades de la población se llama tamaño de la población, y el de la muestra se llama tamaño de muestra. La población y la muestra pueden ser finitas o infinitas y, de manera similar, pueden existir o hipotéticas.

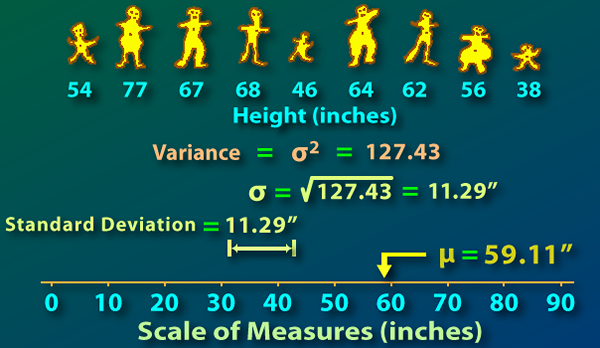
Diferencia: La varianza es un valor numérico que muestra cuán ampliamente las figuras individuales en un conjunto de datos se distribuyen sobre la media. Así es como está cada número de la media y, por lo tanto, de la otra. Una varianza del valor cero significa que todos los datos son idénticos. Más la varianza, más son los valores extendidos sobre la media, por lo tanto, entre sí. Menos la varianza, menos se extienden los valores sobre la media, por lo tanto, y la varianza no puede ser negativa.

Diferencia entre la varianza de la población y la varianza de la muestra

La principal diferencia entre la varianza de la población y la varianza de la muestra se relaciona con el cálculo de la varianza. La varianza se calcula en cinco pasos. Se calcula la primera media, luego calculamos las desviaciones de la media, y en tercer lugar las desviaciones se cuadran, en cuarto lugar, se resumen las desviaciones al cuadrado y finalmente esta suma se divide por el número de elementos para los cuales se calcula la varianza. Así varianza = σ (xi-x-)/n. Donde xi = ith. Número, x- = media y n = número de elementos ..

Ahora, cuando la varianza se calcula a partir de los datos de la población, N es igual al número de elementos. Por lo tanto, si la varianza en la presión arterial de todas las 1000 personas se calculará a partir de datos sobre presiones sanguíneas de todas las 1000 personas, entonces n = 1000. Sin embargo, cuando la varianza se calcula a partir de los datos de la muestra 1, se deducirá de n antes de dividir la suma de las desviaciones al cuadrado. Por lo tanto, en el ejemplo anterior si los datos de la muestra tienen 100 elementos, el denominador sería 100 - 1 = 99.

Debido a esto, el valor de la varianza calculado a partir de los datos de la muestra es mayor que el valor que podría haberse encontrado mediante el uso de datos de población. La lógica de hacerlo es compensar nuestra falta de información sobre los datos de la población. Es imposible descubrir la varianza de las alturas en los seres humanos, porque nuestra falta de información absoluta sobre las alturas de todos los seres humanos vivos, no hablar del futuro. Incluso si tomamos un ejemplo moderado, como los datos de la población sobre las alturas de todos los hombres vivos en nosotros, es físicamente posible, pero el costo y el tiempo involucrados en esto derrotarían el propósito de su cálculo. Esta es la razón por la cual los datos de muestra se toman para la mayoría de los fines estadísticos, y esto se acompaña de la falta de información sobre la mayoría de los datos. Para compensar esto, el valor de la varianza y la desviación estándar, que es la raíz cuadrada de varianza de la varianza, es mayor en el caso de los datos de la muestra que la varianza de los datos de la población.

Esto actúa como un escudo automático para los analistas y tomadores de decisiones. La lógica se aplica a las decisiones sobre presupuesto de capital, finanzas personales y comerciales, construcción, gestión del tráfico y muchos campos aplicables. Esto ayuda a que el billete sea seguro mientras toma una decisión o para otras inferencias.

Resumen: La varianza de la población se refiere al valor de varianza que se calcula a partir de los datos de la población, y la varianza de la muestra es la varianza calculada a partir de datos de la muestra. Debido a este valor de denominador en la fórmula para la varianza en el caso de que los datos de la muestra sean 'N-1', y es 'n' para los datos de la población. Como resultado, tanto la varianza como la desviación estándar derivadas de los datos de la muestra son más que los que se encuentran a partir de los datos de la población.