Diferencias entre la correlación y la regresión

Tanto la correlación como la regresión son herramientas estadísticas que tratan dos o más variables. Aunque ambos se relacionan con el mismo tema, hay diferencias entre los dos. Las diferencias, entre los dos, se explican a continuación.

Significado

El término correlación con referencia a dos o más variables significa que las variables están relacionadas de alguna manera. El análisis de correlación determina si existe una relación entre dos variables y la fuerza de la relación. Si dos variables x (independientes) e y (dependientes) están tan relacionadas que la variación en la magnitud de la variable independiente se acompaña, por variación en la magnitud de la variable dependiente, se dice que las dos variables están correlacionadas.

La correlación puede ser lineal o no lineal. Una correlación lineal es aquella en la que las variables están tan relacionadas que el cambio en el valor de una variable causaría un cambio en el valor de otra variable de manera consistente. En una correlación lineal, los puntos dispersos relacionados con los valores respectivos de variables dependientes e independientes se agruparían alrededor de una línea recta no horizontal, aunque una línea recta horizontal también indicaría una relación lineal entre las variables si una línea recta pudiera conectar los puntos que representan las variables.

El análisis de regresión, por otro lado, utiliza los datos existentes para determinar una relación matemática entre las variables que pueden usarse para determinar el valor de la variable dependiente con respecto a cualquier valor de la variable independiente.

Orientación estadística

La correlación se refiere a la medición de la fuerza de asociación o intensidad de la relación, donde la regresión se refiere a la predicción del valor de la variable dependiente en relación con un valor conocido de la variable independiente. Esto puede explicarse con las siguientes fórmulas.

El coeficiente de correlación o la correlación del coeficiente (R) entre X&Y se descubre con la siguiente fórmula;

r = covarianza (x, y)/σx.σy, cov (x, y) = σxy/n - (σx/n) (σy/n), σx y σy son desviaciones estándar de x e y respectivamente, y -1 < r 0, then correlation coefficient between x and y = correlation coefficient between u and v.

El coeficiente de correlación R es un número puro e independiente de la unidad de medición. Por lo tanto, si x es altura (pulgadas) e y es peso (LBS.) de personas de cierta región, entonces R no está en pulgadas ni en libras., pero simplemente un número.

La ecuación de regresión se encuentra con la siguiente fórmula;

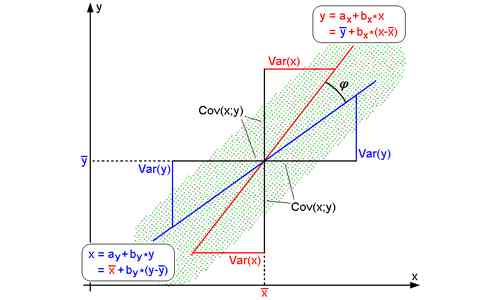
La ecuación de regresión de y en x (para averiguar la estimación de y) es y - y '= byx (x -x‾), BYX se llama coeficiente de regresión de y en x. La ecuación de regresión de x en y (para averiguar la estimación de x) es x - x '= bxy (y -y‾), bxy se llama coeficiente de regresión de x en y.

El análisis de correlación no asume la dependencia de ninguna variable de otra variable, tampoco trata de descubrir la relación entre los dos. Simplemente estima el grado de asociación entre variables. En otras palabras, el análisis de correlación prueba la interdependencia de las variables. El análisis de regresión, por otro lado, describe la dependencia de la variable dependiente o la variable de respuesta en la variable independiente o explicativa/s. El análisis de regresión supone que existe una relación causal unidireccional entre las variables explicativas y de respuesta, y no tiene en cuenta si esa relación causal es positiva o negativa. Para la correlación, los valores de las variables dependientes e independientes son aleatorios, pero para los valores de regresión de variables independientes no necesitan ser aleatorios.

Resumen

1. El análisis de correlación es una prueba de interdependencia entre dos variables. El análisis de regresión proporciona una fórmula matemática para determinar el valor de la variable dependiente con respecto a un valor de variable independiente/s.

2. El coeficiente de correlación es independiente de la elección de origen y escala, pero el coeficiente de regresión no es así.

Para la correlación, los valores de ambas variables deben ser aleatorios, pero esto no es así para el coeficiente de regresión.

Bibliografía

1. Das, N. GRAMO., (1998), Métodos estadísticos, Calcuta

2. Correlación y regresión, disponible en www.lealté.C.A.Reino Unido/bl/gat/virtualfc/stats/regresión

3. Regresión y correlación, disponible en www.abismo.uoregon.edu