Diferencia entre diferenciación e integración

El cálculo es una de las principales aplicaciones matemáticas que se aplican en el mundo hoy para resolver varios fenómenos. Es altamente empleado en estudios científicos, estudios económicos, finanzas e ingeniería, entre otras disciplinas que juegan un papel vital en la vida de un individuo. La integración y la diferenciación son los fundamentos utilizados en el cálculo para estudiar el cambio. Sin embargo, muchas personas, incluidos estudiantes y académicos, no han podido resaltar las diferencias entre la diferenciación y la integración.

¿Qué es la diferenciación??

La diferenciación es un término utilizado en el cálculo para referirse al cambio, qué experiencias de propiedades con respecto a un cambio de unidad en otra propiedad relacionada.

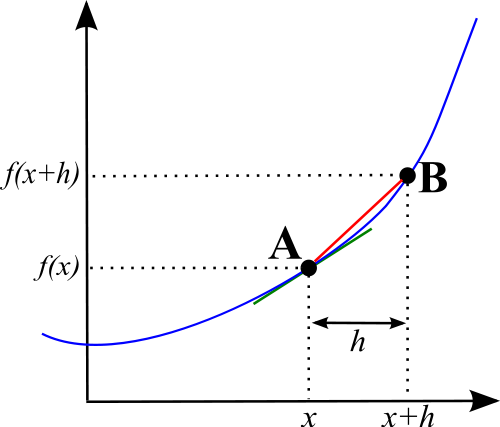
En otro término, la diferenciación forma una expresión algebraica que ayuda en el cálculo del gradiente de una curva en el punto dado. Es importante resaltar que las curvas tienen sus pendientes que varían en el punto dado a diferencia de las líneas rectas, que tienen el mismo gradiente en todo.

¿Qué es la integración??

La integración es un término utilizado en el cálculo para referirse a la fórmula y al procedimiento de calcular el área bajo la curva.

Vale la pena señalar que el gráfico debe estar bajo una curva, lo que resulta en la formación de una parte integral, que es difícil encontrar el área a diferencia de otras formas como círculos, cuadrados y rectángulos, que son más fáciles de calcular sus áreas.

Diferencia entre diferenciación e integración

1) Propósito y funciones de diferenciación e integración

La integración y la diferenciación se pueden diferenciar principalmente en la forma en que se aplican los dos conceptos y sus resultados finales. Se utilizan para llegar a diferentes respuestas, que es la diferencia fundamental. La diferenciación se utiliza para calcular el gradiente de la curva. Las curvas no lineales tienen diferentes pendientes en cualquier punto dado, lo que dificulta determinar sus gradientes. La expresión algebraica utilizada para determinar el cambio incurrido de un punto a otro con una unidad se conoce como diferenciación.  Por otro lado, la integración es una expresión algebraica utilizada para calcular el área debajo de la curva porque no es una forma perfecta después de la cual el área se puede calcular fácilmente.

2) directamente opuesto

Las funciones algebraicas de diferenciación e integración son directamente opuestas entre sí, específicamente en su aplicación. Si uno realiza integración, se dice que él o ella muestra lo contrario de la diferenciación mientras que si se realiza una diferenciación, está realizando opuesto a la integración. Por ejemplo, la integración y la diferenciación forman una relación que se representa de manera similar cuando uno realiza el cuadrado de un número y luego encuentra la raíz cuadrada del resultado. Por lo tanto, si uno quiere encontrar lo contrario de un número integrado, se le pedirá que realice la diferenciación del mismo número. Simplemente, la integración es el proceso inverso de diferenciación y viceversa.

3) Aplicación de la vida real de diferenciación e integración

En escenarios de la vida real, se ha encontrado que la integración y la diferenciación se aplican de manera diferente a cada concepto utilizado para proporcionar diferentes resultados. Sin embargo, es notable resaltar que ambas diferenciación son conceptos de cálculo esenciales que facilitan la vida. Una de las principales aplicaciones de integración es calcular las áreas de superficies curvas, calcular el volumen de objetos y calcular el punto central entre otras funciones.

Por otro lado, el concepto de diferenciación se usa significativamente para calcular la velocidad instantánea y se usa para determinar si una función aumenta o disminuye en consecuencia. Esta es una clara demostración de cómo se aplican los dos conceptos en la vida de las personas.

4) Velocidad y función de la diferenciación e integración

La otra diferencia entre la integración y la diferenciación es el papel que desempeñan cuando se trata de una función dada bajo investigación. Según los matemáticos, la diferenciación ayuda significativamente a determinar la velocidad de la función ayudando en el cálculo de la velocidad instantánea. Por otro lado, la integración se refiere a la determinación de los distanciados recorridos por cualquier función dada. Se estima que el área debajo de la curva es equivalente a la distancia recorrida por la función. La expresión algebraica de integración ayuda a calcular el área bajo la curva, que equivale a la distancia recorrida por la función.

Expresiones/fórmula algebraicas para la diferenciación e integración

También vale la pena señalar que la diferenciación y la integración tienen diferentes expresiones algebraicas, que se utilizan en el cálculo. Esto explica por qué los dos conceptos de cálculo siempre proporcionarán resultados diferentes.  La derivada de una función f (x) con respecto a la variable x y de acuerdo con la regla del producto se definirá como:

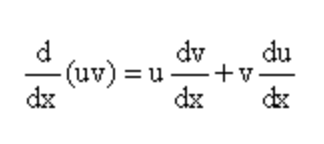
Por otro lado, la fórmula de integración o el área integral debajo de la curva se pueden calcular mediante el uso de la fórmula:

∫f (x) dx, que es la fórmula adoptada bajo el método de sustitución.

5) Adición y división

El otro método para comparar la integración con la diferenciación es explicando específicamente cómo cada función se da cuenta de sus resultados. La integración determina el resultado de una función específica al agregar los aspectos asociados con el cálculo. Por otro lado, la diferenciación determina la velocidad instantánea y la velocidad de la función a través de la división.

Diferencias entre diferenciación e integración: cuadro de comparación

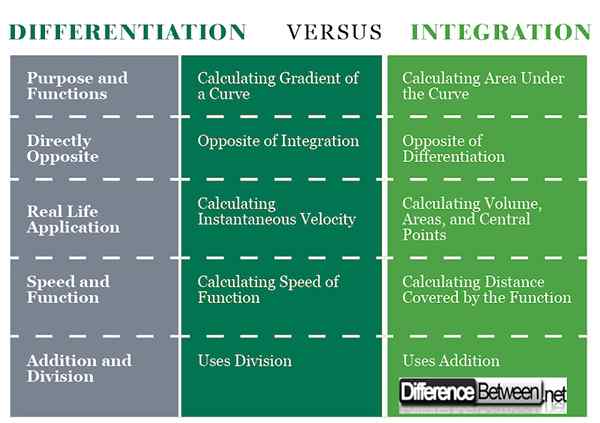
Resumen de la diferenciación vs. Integración

• Una de las principales variaciones entre diferenciación e integración es que las dos funciones de cálculo son directamente opuestas entre sí en su aplicación.
• Los estudiantes y otros académicos deben centrarse en comprender uno de los conceptos después de los cuales deberán realizar lo contrario para determinar los resultados de la otra función.
• Comprender las diferencias que existen entre la integración y la diferenciación son esenciales porque ayudará a las personas a usar la expresión algebraica correcta cuando sea necesario.
• Por último, es vital dominar los dos conceptos de cálculo en matemáticas básicas porque se han utilizado constantemente en diversas disciplinas como economía, negocios e ingeniería.