Diferencia entre integrales definidas e indefinidas

El cálculo es una rama importante de las matemáticas, y la diferenciación juega un papel fundamental en el cálculo. El proceso inverso de la diferenciación se conoce como integración, y el inverso se conoce como la integral, o simplemente la inversa, la inversa de la diferenciación proporciona una integral. En base a los resultados que producen, las integrales se dividen en dos clases a saber., Integrales definidas e indefinidas.

Integral definida

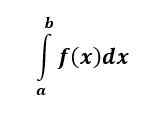
La integral definitiva de F (x) es un número y representa el área bajo la curva F (x) de x = A a x = B.

Una integral definitiva tiene límites superiores e inferiores en las integrales, y se llama definida porque, al final del problema, tenemos un número: es una respuesta definitiva.

Integral indefinida

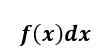
La integral indefinida de F (x) es una función y responde a la pregunta: “Qué función cuando se diferencia da F (x)?"

Con una integral indefinida no hay límites superiores e inferiores en la integral aquí, y lo que obtendremos es una respuesta que todavía tiene Xestá en él y también tendrá una constante (generalmente denotada por C) en eso.

Integral indefinida generalmente ofrece una solución general a la ecuación diferencial.

La integral indefinida es más una forma general de integración, y puede interpretarse como el anti-derivado de la función considerada.

Supongamos que la diferenciación de la función F conduce a otra función F, y la integración de F proporciona la integral. Simbólicamente, esto está escrito como

F (x) = ∫ƒ (x) dx

o

F = ∫ƒ dx

donde ambos F y ƒ son funciones de X, y F es diferenciable. En la forma anterior, se denomina integral de Reimann y la función resultante acompaña a una constante arbitraria.

Una integral indefinida a menudo produce una familia de funciones; Por lo tanto, la integral es indefinida.

Las integrales y el proceso de integración están en el corazón de resolver ecuaciones diferenciales. Sin embargo, a diferencia de los pasos en la diferenciación, los pasos en la integración no siempre siguen una rutina clara y estándar. Ocasionalmente, vemos que la solución no se puede expresar explícitamente en términos de función elemental. En ese caso, la solución analítica a menudo se da en forma de integral indefinida.

Teorema fundamental del cálculo

La integral definitiva e indefinida está vinculado por el teorema fundamental del cálculo de la siguiente manera: para calcular un integral definida, encuentra el integral indefinida (también conocido como anti-derivado) de la función y evaluar en los puntos finales x = A y x = B.

La diferencia entre integrales definidas e indefinidas será evidente una vez que evaluemos las integrales para la misma función.

Considere la siguiente integral:

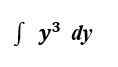
DE ACUERDO. Hagamos ambos y veamos la diferencia.

Para la integración, necesitamos agregar uno al índice que nos lleva a la siguiente expresión:

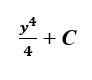
En este momento C es simplemente una constante para nosotros. Se necesita información adicional en el problema para determinar el valor preciso de C.

Evaluemos la misma integral en su forma definitiva I.mi., con los límites superiores e inferiores incluidos.

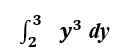
Hablando gráficamente, ahora estamos calculando el área bajo la curva f (x) = y³ entre y = 2 y y = 3.

El primer paso en esta evaluación es el mismo que la evaluación integral indefinida. La única diferencia es que esta vez no agregamos la constante C.

La expresión en este caso se ve de la siguiente manera:

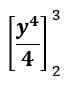
Este giro conduce a:

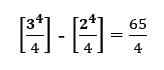
Esencialmente, sustituimos 3 y luego 2 en la expresión y obtuvimos la diferencia entre ellos.

Este es el valor definido en lugar del uso de constante C más temprano.

Explore el factor constante (con respecto a la integral indefinida) con más detalle.

Si el diferencial de Y³ es 3y², entonces

∫3y²dy = y³

Sin embargo, 3y² podría ser el diferencial de muchas expresiones, algunas de las cuales incluyen Y³-5, Y³+7, etc ... Esto implica que la reversión no es única ya que la constante no se cuenta durante la operación.

Entonces en general, 3y² es el diferencial de Y³+C dónde C es cualquier constante. Por cierto, C se conoce como el 'Constante de integración'.

Escribimos esto como:

∫ 3y².dx = y³ + C

Las técnicas de integración para una integral indefinida, como la búsqueda de tabla o la integración de Risch, pueden agregar nuevas discontinuidades durante el proceso de integración. Estas nuevas discontinuidades aparecen porque los anti-derivados pueden requerir la introducción de logaritmos complejos.

Los logaritmos complejos tienen una discontinuidad de salto cuando el argumento cruza el eje real negativo, y los algoritmos de integración a veces no pueden encontrar una representación donde estos saltos se cancelen.

Si la integral definida se evalúa primero calculando una integral indefinida y luego sustituyendo los límites de integración en el resultado, debemos ser conscientes de que la integración indefinida podría producir discontinuidades. Si lo hace, además, debemos investigar las discontinuidades en el intervalo de integración.