Diferencia entre paramétrico y no paramétrico

Los investigadores sociales a menudo construyen una hipótesis, en la que suponen que una cierta regla generalizada puede aplicarse a una población. Proban esta hipótesis utilizando pruebas que pueden ser paramétricas o no paramétricas. Las pruebas paramétricas suelen ser más comunes y se estudian mucho antes como las pruebas estándar utilizadas al realizar investigaciones.

El proceso de realizar una investigación es relativamente simple: construye una hipótesis y supone que una cierta "ley" puede aplicarse a una población. Luego realiza una prueba y recopila datos que luego analiza estadísticamente. Los datos recopilados generalmente pueden representarse como un gráfico, y la ley hipotética como el valor medio de esos datos. Si la ley hipotética y la ley del valor medio coinciden, se confirma la hipótesis.

Sin embargo, en algunos casos, encontrar el valor medio no es la forma más apropiada de buscar la ley. Un gran ejemplo es la distribución del ingreso total. Si no ha coincidido con el valor medio, probablemente se deba a que uno o dos multimillonarios están perturbando sus valores medios. Sin embargo, una mediana dará un resultado mucho más preciso sobre el ingreso promedio que es más probable que coincida con sus datos.

En otras palabras, se utilizará una prueba paramétrica cuando los supuestos hechos sobre la población son claros y hay mucha información disponible al respecto. Las preguntas estarán diseñadas para medir esos parámetros específicos para que los datos se puedan analizar como se describió anteriormente. Se usa una prueba no paramétrica cuando la población probada no se conoce por completo y, por lo tanto, los parámetros examinados también se desconocen. Además, mientras que la prueba paramétrica utiliza valores medios como resultados, la prueba no paramétrica toma la mediana y, por lo tanto, generalmente se utiliza cuando la hipótesis original no se ajusta a los datos.

¿Qué es una prueba paramétrica??

Una prueba paramétrica es una prueba diseñada para proporcionar los datos que luego se analizarán a través de una rama de la ciencia llamada estadística paramétrica. Las estadísticas paramétricas suponen que se conoce cierta información sobre la población, a saber, la distribución de probabilidad. Como ejemplo, la distribución de la altura del cuerpo en todo el mundo se describe mediante un modelo de distribución normal. Similar a eso, cualquier modelo de distribución conocido se puede aplicar a un conjunto de datos. Sin embargo, suponiendo que un determinado modelo de distribución se ajuste a un conjunto de datos significa que se conoce inherentemente cierta información adicional sobre la población, como he mencionado. La distribución de probabilidad contiene diferentes parámetros que describen la forma exacta de la distribución. Estos parámetros son lo que proporcionan las pruebas paramétricas: cada pregunta se adapta para dar un valor exacto de un cierto parámetro para cada individuo entrevistado. Combinado, el valor medio de ese parámetro se usa para la distribución de probabilidad. Eso significa que las pruebas paramétricas también asumen algo sobre la población. Si los supuestos son correctos, las estadísticas paramétricas aplicadas a los datos proporcionados por una prueba paramétrica darán resultados que son mucho más precisos y precisos que el de una prueba y estadísticas no paramétricas.

¿Qué es una prueba no paramétrica??

De manera similar a la prueba y estadísticas paramétricas, existen una prueba y estadísticas no paramétricas. Se usan cuando no se espera que los datos obtenidos se ajusten a una curva de distribución normal o datos ordinales. Un gran ejemplo de datos ordinales es la revisión que deja cuando califica un determinado producto o servicio en una escala del 1 al 5. Los datos ordinales en general se obtienen de las pruebas que utilizan diferentes clasificaciones u órdenes. Por lo tanto, no se basa en números o valores exactos para los parámetros en los que se basaron las pruebas paramétricas en. De hecho, no utiliza parámetros de ninguna manera, porque no asume una determinada distribución. Por lo general, se prefiere un análisis paramétrico a uno no paramétrico, pero si la prueba paramétrica no se puede realizar debido a la población desconocida, es necesario un recurso a pruebas no paramétricas.

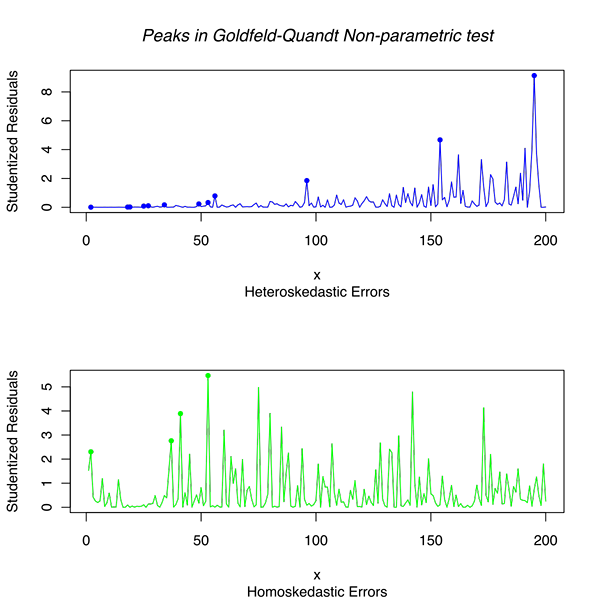
Diferencia entre las pruebas paramétricas y no paramétricas

1) Hacer suposiciones

Como he mencionado, la prueba paramétrica hace suposiciones sobre la población. Necesita los parámetros que están conectados a la distribución normal que se usa en el análisis, y la única forma de conocer estos parámetros es tener algún conocimiento sobre la población. Por otro lado, una prueba no paramétrica, como lo indica el nombre, no depende de ningún parámetro y, por lo tanto, no asume nada sobre la población.

2) probabilidad de paramétrico y no paramétrico

La base del análisis estadístico que se realizará en los datos, en el caso de las pruebas paramétricas, es la distribución probabilística. Por otro lado, la base para las pruebas no paramétricas no existe: es completamente arbitraria. Esto da como resultado más flexibilidad y facilita la hipótesis de los datos recopilados.

3) Medida de tendencia central

La medida de la tendencia central es un valor central en una distribución de probabilidad. Y aunque la distribución de probabilidad en el caso de las estadísticas no paramétricas es arbitraria, todavía existe, y por lo tanto también lo hace la medida de la tendencia central. Sin embargo, esas medidas son diferentes. En el caso de las pruebas paramétricas, se considera el valor medio, mientras que, en el caso de las pruebas no paramétricas, se considera el valor medio.

4) Conocimiento de los parámetros de población

Como he mencionado en la primera diferencia, la información sobre la población varía entre las pruebas y estadísticas paramétricas y no paramétricas. A saber, cierto conocimiento sobre la población es absolutamente necesario para un análisis paramétrico, ya que requiere parámetros relacionados con la población para dar resultados precisos. Por otro lado, se puede adoptar un enfoque no paramétrico sin ningún conocimiento previo de la población.

Paramétrico VS. Pruebas no paramétricas: tabla de comparación

Resumen de paramétrico y no paramétrico

• Una prueba paramétrica es una prueba que supone que ciertos parámetros y distribuciones se conocen sobre una población, contraria a la no paramétrica
• La prueba paramétrica utiliza un valor medio, mientras que la no paramétrica usa un valor medio
• El enfoque paramétrico requiere un conocimiento previo sobre la población, contrario al enfoque no paramétrico