Diferencia entre la prueba paramétrica y no paramétrica
- 3859
- 1193
- Pablo Carranza
Para hacer la generalización sobre la población de la muestra, se utilizan pruebas estadísticas. Una prueba estadística es una técnica formal que se basa en la distribución de probabilidad, para llegar a la conclusión sobre la razonabilidad de la hipótesis. Estas pruebas hipotéticas relacionadas con las diferencias se clasifican como pruebas paramétricas y no paramétricas.El prueba paramétrica es uno que tiene información sobre el parámetro de población.
Por otro lado, el prueba no paramétrica es uno en el que el investigador no tiene idea del parámetro de población. Entonces, tome una lectura completa de este artículo, para conocer las diferencias significativas entre la prueba paramétrica y no paramétrica.
Contenido: prueba paramétrica versus prueba no paramétrica
- Cuadro comparativo
- Definición
- Diferencias clave
- Jerarquía de pruebas de hipótesis
- Pruebas equivalentes
- Conclusión
Cuadro comparativo
| Base para la comparación | Prueba paramétrica | Prueba no paramétrica |
|---|---|---|
| Significado | Una prueba estadística, en la que se hacen suposiciones específicas sobre el parámetro de población se conoce como prueba paramétrica. | Una prueba estadística utilizada en el caso de variables independientes no métricas se llama prueba no paramétrica. |
| Base de estadística de prueba | Distribución | Arbitrario |
| Nivel de medición | Intervalo o relación | Nominal u ordinal |
| Medida de tendencia central | Significar | Mediana |
| Información sobre la población | Completamente conocido | Indisponible |
| Aplicabilidad | Variables | Variables y atributos |
| Prueba de correlación | Perea | Lancero |
Definición de prueba paramétrica
La prueba paramétrica es la prueba de hipótesis que proporciona generalizaciones para hacer declaraciones sobre la media de la población principal. Una prueba t basada en la estadística t de Student, que a menudo se usa a este respecto.
La estadística t se basa en la suposición subyacente de que existe la distribución normal de la variable y la media conocida o se supone que se sabe. La varianza de la población se calcula para la muestra. Se supone que las variables de interés, en la población se miden en una escala de intervalo.
Definición de prueba no paramétrica
La prueba no paramétrica se define como la prueba de hipótesis que no se basa en suposiciones subyacentes, i.mi. no requiere que la distribución de la población se denote por parámetros específicos.
La prueba se basa principalmente en diferencias en las medianas. Por lo tanto, se conoce alternativamente como la prueba sin distribución. La prueba supone que las variables se miden a nivel nominal u ordinal. Se usa cuando las variables independientes no son métricas.
Diferencias clave entre las pruebas paramétricas y no paramétricas
Las diferencias fundamentales entre la prueba paramétrica y no paramétrica se discuten en los siguientes puntos:
- Una prueba estadística, en la que se hacen suposiciones específicas sobre el parámetro de población se conoce como prueba paramétrica. Una prueba estadística utilizada en el caso de variables independientes no métricas se llama prueba no paramétrica.
- En la prueba paramétrica, el estadístico de prueba se basa en la distribución. Por otro lado, la estadística de prueba es arbitraria en el caso de la prueba no paramétrica.
- En la prueba paramétrica, se supone que la medición de las variables de interés se realiza a nivel de intervalo o relación. A diferencia de la prueba no paramétrica, en la que la variable de interés se mide a escala nominal u ordinal.
- En general, la medida de la tendencia central en la prueba paramétrica es media, mientras que en el caso de la prueba no paramétrica es media.
- En la prueba paramétrica, hay información completa sobre la población. Por el contrario, en la prueba no paramétrica, no hay información sobre la población.
- La aplicabilidad de la prueba paramétrica es solo para variables, mientras que la prueba no paramétrica se aplica tanto a las variables como a los atributos.
- Para medir el grado de asociación entre dos variables cuantitativas, el coeficiente de correlación de Pearson se usa en la prueba paramétrica, mientras que la correlación de rango de Spearman se usa en la prueba no paramétrica.
Jerarquía de pruebas de hipótesis
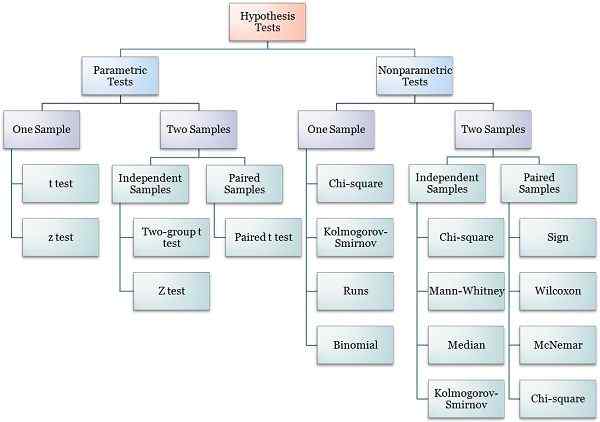
Pruebas equivalentes
| Prueba paramétrica | Prueba no paramétrica |
|---|---|
| Prueba t de muestra independiente | Prueba de Mann-Whitney |
| Prueba de muestras emparejadas t | Prueba de rango firmada de Wilcoxon |
| Análisis de varianza de una manera (ANOVA) | Prueba de Kruskal Wallis |
| Análisis de varianza de medidas repetidas | ANOVA de Friedman |
Conclusión
Tomar una elección entre la prueba paramétrica y no paramétrica no es fácil para un investigador que realice un análisis estadístico. Para realizar una hipótesis, si la información sobre la población se conoce completamente, a modo de parámetros, entonces se dice que la prueba es una prueba paramétrica, mientras que, si no hay conocimiento sobre la población y es necesario probar la hipótesis de la población, entonces el La prueba realizada se considera como la prueba no paramétrica.