Diferencia entre la prueba t y la prueba F

- 1025
- 83
- Pablo Carranza
 Las pruebas de hipótesis comienzan con la configuración de las premisas, que se sigue seleccionando un nivel de significancia. A continuación, tenemos que elegir la estadística de prueba, yo.mi. prueba t o prueba f. Mientras prueba t se usa para comparar dos muestras relacionadas, prueba F se usa para probar la igualdad de dos poblaciones.
Las pruebas de hipótesis comienzan con la configuración de las premisas, que se sigue seleccionando un nivel de significancia. A continuación, tenemos que elegir la estadística de prueba, yo.mi. prueba t o prueba f. Mientras prueba t se usa para comparar dos muestras relacionadas, prueba F se usa para probar la igualdad de dos poblaciones.
La hipótesis es una proposición simple que puede probarse o refutarse a través de varias técnicas científicas y establece la relación entre una variable independiente y una variable dependiente. Es capaz de ser probado y verificado para determinar su validez, mediante un examen imparcial. La prueba de una hipótesis intenta dejar en claro, si la suposición es válida o no.
Para un investigador, es imperativo elegir la prueba correcta para su hipótesis como la decisión completa de validar o rechazar la hipótesis nula se basa en ella. Lea el artículo dado para comprender la diferencia entre la prueba t y la prueba F.
Contenido: Test T Vs F-Test
- Cuadro comparativo
- Definición
- Diferencias clave
- Conclusión
Cuadro comparativo
| Base para la comparación | Prueba t | Prueba F |
|---|---|---|
| Significado | La prueba t es una prueba de hipótesis univariada, que se aplica cuando no se conoce la desviación estándar y el tamaño de la muestra es pequeño. | La prueba F es una prueba estadística, que determina la igualdad de las variaciones de las dos poblaciones normales. |
| Estadística de prueba | T-estadística sigue a la distribución t de Student, bajo hipótesis nula. | F-estadística sigue a Snedecor F-Distribution, bajo hipótesis nula. |
| Solicitud | Comparando los medios de dos poblaciones. | Comparando dos variaciones de población. |
Definición de prueba t
Una prueba t es una forma de la prueba de hipótesis estadística, basada en la estadística T del estudiante y la distribución T para descubrir el valor p (probabilidad) que puede usarse para aceptar o rechazar la hipótesis nula.
Análisis de prueba t Si los medios de dos conjuntos de datos son muy diferentes entre sí, yo.mi. si la media de la población es igual o diferente de la media estándar. También se puede usar para determinar si la línea de regresión tiene una pendiente diferente de cero. La prueba se basa en una serie de supuestos, que son:
- La población es infinita y normal.
- La varianza de la población es desconocida y estimada a partir de la muestra.
- La media se conoce.
- Las observaciones de la muestra son aleatorias e independientes.
- El tamaño de la muestra es pequeño.
- H0 puede ser un lado o dos lados.
La media y la desviación estándar de la dos muestra se utilizan para hacer una comparación entre ellos, de modo que:
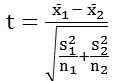 dónde,
dónde,
X1 = Media del primer conjunto de datos
x̄2 = media del segundo conjunto de datos
S1 = Desviación estándar del primer conjunto de datos
S2 = Desviación estándar del segundo conjunto de datos
norte1 = Tamaño del primer conjunto de datos
norte2 = Tamaño del segundo conjunto de datos
Definición de prueba F
La prueba F se describe como un tipo de prueba de hipótesis, que se basa en la distribución F Snedecor, bajo la hipótesis nula. La prueba se realiza cuando no se sabe si las dos poblaciones tienen la misma varianza.
La prueba F también se puede utilizar para verificar si los datos se ajustan a un modelo de regresión, que se adquiere a través del análisis de mínimo cuadrado. Cuando hay un análisis de regresión lineal múltiple, examina la validez general del modelo o determina si alguna de las variables independientes está teniendo una relación lineal con la variable dependiente. Se pueden hacer una serie de predicciones, la comparación de los dos conjuntos de datos. La expresión del valor de la prueba F está en la relación de variaciones de las dos observaciones, que se muestra como debajo:
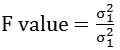 Donde, σ2 = Varianza
Donde, σ2 = Varianza
Los supuestos sobre los que se basa la prueba F son:
- La población se distribuye normalmente.
- Se han dibujado muestras al azar.
- Las observaciones son independientes.
- H0 puede ser un lado o dos lados.
Diferencias clave entre la prueba t y la prueba F
La diferencia entre la prueba t y la prueba F se puede dibujar claramente por los siguientes motivos:
- Una prueba de hipótesis univariada que se aplica cuando no se conoce la desviación estándar y el tamaño de la muestra es pequeño es una prueba t. Por otro lado, una prueba estadística, que determina la igualdad de las variaciones de los dos conjuntos de datos normales, se conoce como prueba F.
- La prueba t se basa en la estadística T, sigue a la distribución t de Student, bajo la hipótesis nula. Por el contrario, la base de la prueba F es F-Stadistic sigue a Snedecor F-Distribution, bajo la hipótesis nula.
- La prueba t se usa para comparar los medios de dos poblaciones. En contraste, la prueba F se usa para comparar dos variaciones de población.
Conclusión
La prueba t y la prueba F son los dos, del número de diferentes tipos de prueba estadística utilizadas para las pruebas de hipótesis y decide si vamos a aceptar la hipótesis nula o lo rechazaremos. La prueba de hipótesis no toma las decisiones en sí, sino que ayuda al investigador a la toma de decisiones.
- « Diferencia entre la prueba paramétrica y no paramétrica
- Diferencia entre la varianza y la desviación estándar »

