Diferencia entre la varianza y la desviación estándar

- 2235
- 478
- Horacio Apodaca
 La dispersión indica la medida en que las observaciones se desvían de una medida apropiada de la tendencia central. Las medidas de dispersión se dividen en dos categorías I.mi. una medida absoluta de dispersión y medida relativa de dispersión. La varianza y la desviación estándar son dos tipos de una medida absoluta de variabilidad; que describe cómo las observaciones se extienden alrededor de la media. Diferencia no es más que el promedio de los cuadrados de las desviaciones,
La dispersión indica la medida en que las observaciones se desvían de una medida apropiada de la tendencia central. Las medidas de dispersión se dividen en dos categorías I.mi. una medida absoluta de dispersión y medida relativa de dispersión. La varianza y la desviación estándar son dos tipos de una medida absoluta de variabilidad; que describe cómo las observaciones se extienden alrededor de la media. Diferencia no es más que el promedio de los cuadrados de las desviaciones,
A diferencia de, Desviación Estándar es la raíz cuadrada del valor numérico obtenido al calcular la varianza. Muchas personas contrastan estos dos conceptos matemáticos. Entonces, este artículo intenta arrojar luz sobre la importante diferencia entre la varianza y la desviación estándar.
Contenido: varianza vs desviación estándar
- Cuadro comparativo
- Definición
- Diferencias clave
- Ilustración
- Similitudes
- Conclusión
Cuadro comparativo
| Base para la comparación | Diferencia | Desviación Estándar |
|---|---|---|
| Significado | La varianza es un valor numérico que describe la variabilidad de las observaciones de su media aritmética. | La desviación estándar es una medida de dispersión de observaciones dentro de un conjunto de datos. |
| Qué es? | Es el promedio de las desviaciones al cuadrado. | Es la raíz media de la desviación cuadrada. |
| Etiquetado como | Sigma cuadrado (σ^2) | Sigma (σ) |
| Expresado en | Unidades cuadradas | Las mismas unidades que los valores en el conjunto de datos. |
| Indica | ¿Hasta dónde se extienden las personas en un grupo?. | Cuántas observaciones de un conjunto de datos difieren de su media. |
Definición de varianza
En las estadísticas, la varianza se define como la medida de variabilidad que representa hasta qué punto se extienden los miembros de un grupo. Descubre el grado promedio al que cada observación varía de la media. Cuando la varianza de un conjunto de datos es pequeña, muestra la cercanía de los puntos de datos a la media, mientras que un mayor valor de varianza representa que las observaciones están muy dispersas alrededor de la media aritmética y entre sí.
Para datos no clasificados: 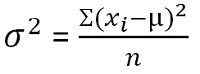
Para distribución de frecuencia agrupada: 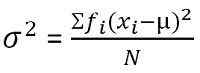
Definición de desviación estándar
La desviación estándar es una medida que cuantifica la cantidad de dispersión de las observaciones en un conjunto de datos. La desviación estándar baja es un indicador de la cercanía de las puntuaciones a la media aritmética y representa una desviación estándar alta; Los puntajes se dispersan en un rango más alto de valores.
Para datos no clasificados: 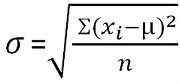 Para distribución de frecuencia agrupada:
Para distribución de frecuencia agrupada: 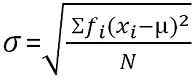
Diferencias clave entre la varianza y la desviación estándar
La diferencia entre la desviación estándar y la varianza se puede dibujar claramente por los siguientes motivos:
- La varianza es un valor numérico que describe la variabilidad de las observaciones de su media aritmética. La desviación estándar es una medida de la dispersión de observaciones dentro de un conjunto de datos en relación con su media.
- La varianza no es más que un promedio de desviaciones al cuadrado. Por otro lado, la desviación estándar es la desviación cuadrada media de la raíz.
- La varianza se denota por Sigma Squared (σ2) mientras que la desviación estándar se etiqueta como Sigma (σ).
- La varianza se expresa en unidades cuadradas que generalmente son mayores que los valores en el conjunto de datos dado. A diferencia de la desviación estándar que se expresa en las mismas unidades que los valores en el conjunto de datos.
- Medidas de varianza hasta qué punto se extienden las personas en un grupo en el conjunto de datos del promedio. Por el contrario, la desviación estándar mide cuántas observaciones de un conjunto de datos difieren de su media.
Ilustración
Las marcas calificadas por un estudiante en cinco materias son 60, 75, 46, 58 y 80 respectivamente. Tienes que averiguar la desviación y la varianza estándar.
En primer lugar, tienes que averiguar la media,
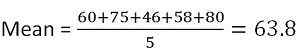
Entonces las marcas promedio (media) son 63.8
Ahora calcule la varianza
| X | A | (X-A) | (X-A)^2 |
|---|---|---|---|
| 60 | 63.8 | -3.8 | 14.44 |
| 75 | 63.8 | 11.2 | 125.44 |
| 46 | 63.8 | -17.8 | 316.84 |
| 58 | 63.8 | 5.8 | 33.64 |
| 80 | 63.8 | dieciséis.2 | 262.44 |
Donde, x = observaciones
A = media aritmética
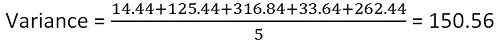 Entonces la varianza es 150.56
Entonces la varianza es 150.56
Y la desviación estándar es - 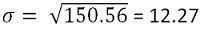
Similitudes
- Tanto la varianza como la desviación estándar son siempre positivas.
- Si todas las observaciones en un conjunto de datos son idénticas, entonces la desviación estándar y la varianza serán cero.
Conclusión
Estos dos son términos estadísticos básicos, que están desempeñando un papel vital en diferentes sectores. La desviación estándar se prefiere sobre la media, ya que se expresa en las mismas unidades que las de las mediciones, mientras que la varianza se expresa en las unidades más grandes que el conjunto de datos dado.

