Diferencia entre la relación y la proporción

- 3683
- 940
- Florencia Galindo
 La relación y la proporción son dos conceptos matemáticos que tienen un número final de aplicaciones prácticas en diferentes esferas de la vida. El relación se utiliza para comparar las cantidades de dos categorías diferentes como la proporción de hombres con mujeres en la ciudad. Aquí, hombres y mujeres son las dos categorías diferentes.
La relación y la proporción son dos conceptos matemáticos que tienen un número final de aplicaciones prácticas en diferentes esferas de la vida. El relación se utiliza para comparar las cantidades de dos categorías diferentes como la proporción de hombres con mujeres en la ciudad. Aquí, hombres y mujeres son las dos categorías diferentes.
De lo contrario, Proporción se usa para descubrir la cantidad de una categoría sobre el total, como la proporción de hombres de las personas totales que viven en la ciudad.
La relación define la relación cuantitativa entre dos cantidades, lo que representa el número de tiempo que un valor contiene el otro. Por el contrario, la proporción es esa parte que explica la relación comparativa con toda la parte. Este artículo le presenta las diferencias básicas entre la relación y la proporción. Echar un vistazo.
Contenido: Ratio vs proporción
- Cuadro comparativo
- Definición
- Diferencias clave
- Ejemplo
- Conclusión
Cuadro comparativo
| Base para la comparación | Relación | Proporción |
|---|---|---|
| Significado | La relación se refiere a la comparación de dos valores de la misma unidad. | Cuando dos proporciones se establecen iguales entre sí, se denomina proporción. |
| Qué es? | Expresión | Ecuación |
| Denotado por | Colon (:) firma | Doble colon (: :) o igual al (=) signo |
| Representa | Relación cuantitativa entre dos categorías. | Relación cuantitativa de una categoría y el total |
| Palabra clave | 'A cada' | 'Fuera de' |
Definición de relación
En matemáticas, la relación se describe como la comparación del tamaño de dos cantidades de la misma unidad, que se expresa en términos de tiempos i.mi. el número de veces el primer valor contiene el segundo. Se expresa en su forma más simple. Las dos cantidades en comparación se llaman Términos de relación, donde está el primer término antecedente Y el segundo término es consiguiente.
Por ejemplo: 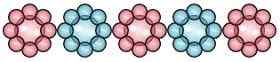 En la figura dada, hay 3 flores rojos a 2 flores azules, yo.mi. 3: 2. Entonces 3 y 2 son dos cantidades de la misma unidad, la fracción de estas dos cantidades (3/2) se conoce como su relación. Aquí, 3 y 2 son los términos de la relación, donde 3 es antecedente, mientras que 2 es consecuente.
En la figura dada, hay 3 flores rojos a 2 flores azules, yo.mi. 3: 2. Entonces 3 y 2 son dos cantidades de la misma unidad, la fracción de estas dos cantidades (3/2) se conoce como su relación. Aquí, 3 y 2 son los términos de la relación, donde 3 es antecedente, mientras que 2 es consecuente.
Hay pocos puntos para recordar en relación con la proporción, que se menciona como:
- Tanto el antecedente como el consecuente pueden multiplicarse por el mismo número. El número debe ser distinto de cero.
- El orden de los términos es significativo.
- La existencia de la relación es solo entre las cantidades del mismo tipo.
- La unidad de las cantidades en comparación también debe ser la misma.
- La comparación de dos proporciones solo se puede hacer si son equivalentes como la fracción.
Definición de proporción
La proporción es un concepto matemático, que establece la igualdad de dos proporciones o fracciones. Se refiere a una categoría sobre el total. Cuando dos conjuntos de números, aumentan o disminuyen en la misma relación, se dice que son directamente proporcionales entre sí.
Por ejemplo,  1 de 3 flores es roja = 2 de 6 flores es roja.
1 de 3 flores es roja = 2 de 6 flores es roja.
Se consideran que cuatro números P, Q, R, S están en proporción si P: Q = R: S, entonces P/Q = R/S, I.mi. ps = qr (por regla de multiplicación cruzada). Aquí P, Q, R, S se llaman el Términos de proporción, en el que P es el primer término, Q es el segundo término, R es el tercer término y S es el cuarto término. El primer y cuarto término se llaman extremos mientras se llaman el segundo y tercer término medio i.mi. termino medio. Además, si hay tres cantidades en proporción continua, entonces la segunda cantidad es la proporción media entre la primera y la tercera cantidad.
Las propiedades importantes de la proporción se analizan a continuación:
- Invertendo - si p: q = r: s, entonces q: p = s: r
- Alternendo - If P: Q = R: S, entonces P: R = Q: S
- Componente - If P: Q = R: S, entonces P + Q: Q = R + S: S
- Dividendo - si p: q = r: s, entonces p - q: q = r - s: s
- Componente y dividendo - If P: Q = R: S, entonces P + Q: P - Q = R + S: R - S
- Addendo - If P: Q = R: S, entonces P + R: Q + S
- Subtrahendo - if p: q = r: s, entonces p - r: q - s
Diferencias clave entre la relación y la proporción
La diferencia entre la relación y la proporción se puede dibujar claramente por los siguientes motivos:
- La relación se define como la comparación de tamaños de dos cantidades de la misma unidad. La proporción, por otro lado, se refiere a la igualdad de dos proporciones.
- La relación es una expresión, mientras que la proporción es una ecuación que se puede resolver.
- La relación está representada por colon (:) signo entre las cantidades comparadas. En proporción de contraste, se denota con doble colon (: :) o igual al signo (=), entre las proporciones en comparación.
- La relación representa la relación cuantitativa entre dos categorías. A diferencia de la proporción, que muestra la relación cuantitativa de una categoría con el total.
- En un problema dado, puede identificar si están en relación o proporción, con la ayuda de palabras clave que usan i.mi. 'a cada' en relación y 'fuera de' en el caso de la proporción.
Ejemplo
Hay un total de 80 estudiantes en clase, de los cuales 30 son niños y el resto de los estudiantes son niñas. Ahora descubra lo siguiente:
(i) Relación de niños a niñas y niñas a niños
(ii) proporción de niños y niñas en la clase
Solución: (i) Relación de niños a niñas = niños: niñas = 30:50 o 3: 5
Ratio de niñas a niños = niñas: niños = 50: 30 o 5: 3
Por lo tanto, por cada tres niños hay cinco niñas o por cada cinco niñas, hay tres niños.
(ii) proporción de niños = 30/80 o 3/8
Proporción de niñas = 50/80 o 5/8
Por lo tanto, 3 de cada 8 estudiantes son un niño y 5 de cada 8 estudiantes es una niña.
Conclusión
Por lo tanto, con la discusión y los ejemplos anteriores, uno puede comprender fácilmente las diferencias entre estos dos conceptos matemáticos. La relación es la comparación de dos números, mientras que la proporción no es más que una extensión sobre la relación que establece que dos relaciones o fracción son equivalentes.
- « Diferencia entre el costo del producto y el costo del período
- Diferencia entre activos y pasivos »

