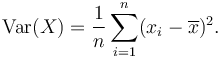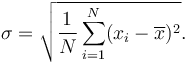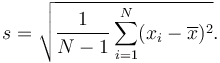Desviación estándar vs. Diferencia
- 1373
- 280
- Pablo Carranza
Desviación Estándar y diferencia son medidas estadísticas de dispersión de datos, yo.mi., Representan cuánta variación hay del promedio, o en qué medida los valores típicamente se "desvían" de la media (promedio). Una varianza o desviación estándar de cero indica que todos los valores son idénticos.
La varianza es la media de los cuadrados de las desviaciones (i.mi., diferencia en los valores de la media), y la desviación estándar es la raíz cuadrada de esa varianza. La desviación estándar se utiliza para identificar valores atípicos en los datos.
Cuadro comparativo
Diferencias - similitudes -| Desviación Estándar | Diferencia | |
|---|---|---|
| Fórmula matemática | Raíz cuadrada de varianza | Promedio de los cuadrados de desviaciones de cada valor de la media en una muestra. |
| Símbolo | Carta griega Sigma - σ | Sin símbolo dedicado; expresado en términos de desviación estándar u otros valores. |
| Valores en relación con el conjunto de datos dado | La misma escala que los valores en el conjunto de datos dado; Por lo tanto, expresado en las mismas unidades. | Escala mayor que los valores en el conjunto de datos dado; no se expresa en la misma unidad que los valores mismos. |
| Son valores negativos o positivos? | Siempre no negativo | Siempre no negativo |
| Aplicación del mundo real | Muestreo de población; Identificación de valores atípicos | Fórmulas estadísticas, finanzas. |
Conceptos importantes
- Significar: El promedio de todos los valores en un conjunto de datos (agregue todos los valores y divida su suma por el número de valores).
- Desviación: la distancia de cada valor de la media. Si la media es 3, un valor de 5 tiene una desviación de 2 (reste la media del valor). La desviación puede ser positiva o negativa.
Símbolo
La fórmula para la desviación y la varianza estándar a menudo se expresa usando:
- x̅ = la media o promedio de todos los puntos de datos en el problema
- X = un punto de datos individual
- N = el número de puntos en el conjunto de datos
- ∑ = La suma de [los cuadrados de las desviaciones]
Fórmulas
La varianza de un conjunto de norte Los valores igualmente probables se pueden escribir como:
La desviación estándar es la raíz cuadrada de la varianza:
Las fórmulas con letras griegas tienen una forma de parecer desalentador, pero esto menos complicado de lo que parece. Para ponerlo en simples pasos:
- Encuentre el promedio de todos los puntos de datos
- Descubra qué tan lejos está cada punto del promedio (esta es la desviación)
- cuadrado cada desviación (yo.mi. la diferencia de cada valor de la media)
- divide la suma de los cuadrados por el número de puntos.
Que da la varianza. Tome la raíz cuadrada de la varianza para encontrar la desviación estándar.
Este excelente video de Khan Academy explica los conceptos de varianza y desviación estándar:
Ejemplo
Digamos que un conjunto de datos incluye la altura de seis diente de león: 3 pulgadas, 4 pulgadas, 5 pulgadas, 4 pulgadas, 11 pulgadas y 6 pulgadas.
Primero, encuentre la media de los puntos de datos: (3 + 4 + 5 + 4 + 11 + 7) / 6 = 5.5
Entonces la altura media es 5.5 pulgadas. Ahora necesitamos las desviaciones, por lo que encontramos la diferencia de cada planta de la media: -2.5, -1.5, -.5, -1.5, 5.5, 1.5
Ahora cuadrado cada desviación y encuentre su suma: 6.25 + 2.25 + .25 + 2.25 + 30.25 + 2.25 = 43.5
Ahora divida la suma de los cuadrados por el número de puntos de datos, en este caso plantas: 43.5/6 = 7.25
Entonces, la varianza de este conjunto de datos es 7.25, que es un número bastante arbitrario. Para convertirlo en una medición del mundo real, tome la raíz cuadrada de 7.25 para encontrar la desviación estándar en pulgadas.
La desviación estándar es de aproximadamente 2.69 pulgadas. Eso significa que para la muestra, cualquier diente de león dentro de 2.69 pulgadas de la media (5.5 pulgadas) es 'normal'.
Por qué cuadrar las desviaciones?
Las desviaciones se cuadran para evitar valores negativos (desviaciones por debajo de la media) de cancelar los valores positivos. Esto funciona porque un número negativo al cuadrado se convierte en un valor positivo. Si tuvo un conjunto de datos simple con desviaciones de la media de +5, +2, -1 y -6, la suma de las desviaciones saldrá como cero si los valores no están cuadrados (i.mi. 5 + 2 - 1 - 6 = 0).
Aplicaciones del mundo real
La varianza se expresa como una dispersión matemática. Dado que es un número arbitrario en relación con las mediciones originales del conjunto de datos, es difícil visualizar y aplicar en un sentido del mundo real. Encontrar la varianza suele ser solo el paso final antes de encontrar la desviación estándar. Los valores de varianza a veces se usan en fórmulas finanzas y estadísticas.
La desviación estándar, que se expresa en las unidades originales del conjunto de datos, es mucho más intuitiva y más cercana a los valores del conjunto de datos original. Se usa con mayor frecuencia para analizar muestras demográficas o de población para obtener una idea de lo que es normal en la población.
Encontrar valores atípicos
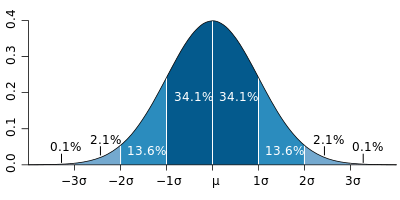Una distribución normal (curva de campana) con bandas correspondientes a 1σ En una distribución normal, aproximadamente el 68% de la población (o valores) cae dentro de 1 desviación estándar (1σ) de la media y aproximadamente el 94% caen dentro de 2σ. Valores que difieren de la media por 1.7σ o más generalmente se consideran valores atípicos.
En la práctica, los sistemas de calidad como Six Sigma intentan reducir la tasa de errores para que los errores se conviertan en un valor atípico. El término "proceso Six Sigma" proviene de la noción de que si uno tiene seis desviaciones estándar entre la media del proceso y el límite de especificación más cercano, prácticamente ningún elemento no cumplirá con las especificaciones.[1]
Muestra de desviación estándar
En aplicaciones del mundo real, los conjuntos de datos utilizados generalmente representan muestras de población, en lugar de poblaciones enteras. Se utiliza una fórmula ligeramente modificada si se deben extraer conclusiones de la población de una muestra parcial.
Se utiliza una 'desviación estándar de muestra' si todo lo que tiene es una muestra, pero desea hacer una declaración sobre la desviación estándar de la población a partir de la cual se extrae la muestra
La única forma en que la fórmula de desviación estándar de muestra difiere de la fórmula de desviación estándar es el "-1" en el denominador.
Usando el ejemplo de diente de león, se necesitaría esta fórmula si probáramos solo 6 diente de león, pero queríamos usar esa muestra para indicar la desviación estándar de todo el campo con cientos de diente de león.
La suma de cuadrados ahora se dividiría por 5 en lugar de 6 (n - 1), lo que da una varianza de 8.7 (en lugar de 7.25), y una desviación estándar de muestra de 2.95 pulgadas, en lugar de 2.69 pulgadas para la desviación estándar original. Este cambio se utiliza para encontrar un margen de error en una muestra (9% en este caso).