Diferencia entre la distribución binomial y de Poisson

- 3463
- 881
- Juan Carlos Rodrígez
 El Distribución binomial es uno, cuyo posible número de resultados son dos, yo.mi. éxito o fracaso. Por otro lado, no hay límite de posibles resultados en distribución de veneno
El Distribución binomial es uno, cuyo posible número de resultados son dos, yo.mi. éxito o fracaso. Por otro lado, no hay límite de posibles resultados en distribución de veneno
La distribución de probabilidad teórica se define como una función que asigna una probabilidad a cada posible resultados del experimento estadístico. La distribución de probabilidad puede ser discreta o continua, donde, en la variable aleatoria discreta, la probabilidad total se asigna a diferentes puntos de masa, mientras que en la variable aleatoria continua la probabilidad se distribuye a varios intervalos de clase.
La distribución binomial y la distribución de Poisson son dos distribución de probabilidad discreta. La distribución normal, la distribución del alumno, la distribución de chi-cuadrado y la distribución F son los tipos de variables aleatorias continuas. Entonces, aquí vamos a discutir la diferencia entre Binomial y Poisson Distribution. Echar un vistazo.
Contenido: distribución binomial vs Poisson Distribución
- Cuadro comparativo
- Definición
- Diferencias clave
- Conclusión
Cuadro comparativo
| Base para la comparación | Distribución binomial | Distribución de veneno |
|---|---|---|
| Significado | La distribución binomial es aquella en la que se estudian la probabilidad de un número repetido de ensayos. | La distribución de Poisson da que el recuento de eventos independientes ocurra aleatoriamente con un período de tiempo determinado. |
| Naturaleza | Biparamétrico | Uniparamétrico |
| Número de intentos | Fijado | Infinito |
| Éxito | Probabilidad constante | Posibilidad infinitesimal de éxito |
| Resultados | Solo dos resultados posibles, yo.mi. éxito o fracaso. | Número ilimitado de resultados posibles. |
| Media y varianza | Media> Varianza | Media = varianza |
| Ejemplo | Experimento de lanzamiento de monedas. | Impresión de errores/página de un libro grande. |
Definición de distribución binomial
La distribución binomial es la distribución de probabilidad ampliamente utilizada, derivada del proceso de Bernoulli (un experimento aleatorio que lleva el nombre de un famoso matemático Bernoulli). También se conoce como distribución biparamétrica, ya que aparece por dos parámetros N y P. Aquí, n es las pruebas repetidas y P es la probabilidad de éxito. Si se conoce el valor de estos dos parámetros, significa que la distribución es completamente conocida. La media y la varianza de la distribución binomial se denotan por µ = NP y σ2 = NPQ.
P (x = x) = norteCX pagX QN-X, x = 0,1,2,3 ... n
= 0, de lo contrario
Un intento de producir un resultado particular, que no es nada seguro e imposible, se llama juicio. Los ensayos son independientes y un entero positivo fijo. Está relacionado con dos eventos mutuamente excluyentes y exhaustivos; en el que la ocurrencia se llama éxito y la no ocurrencia se llama falla. P representa la probabilidad de éxito, mientras que Q = 1 - P representa la probabilidad de falla, que no cambia a lo largo del proceso.
Definición de distribución de Poisson
A fines de la década de 1830, un famoso matemático francés Simon Denis Poisson presentó esta distribución. Describe la probabilidad de que el cierto número de eventos ocurran en un intervalo de tiempo fijo. Es una distribución uniparamétrica, ya que aparece solo por un parámetro λ o m. En Poisson Distribution Media se denota por M I.mi. µ = m o λ y la varianza se etiqueta como σ2 = m o λ. La función de masa de probabilidad de X está representada por:
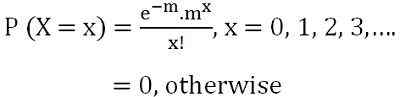 donde e = cantidad trascendental, cuyo valor aproximado es 2.71828
donde e = cantidad trascendental, cuyo valor aproximado es 2.71828
Cuando el número del evento es alto pero la probabilidad de su ocurrencia es bastante baja, se aplica la distribución de Poisson. Como por ejemplo, el número de reclamos de seguro/día en una compañía de seguros.
Diferencias clave entre la distribución binomial y de Poisson
Las diferencias entre la distribución binomial y de Poisson se pueden dibujar claramente por los siguientes motivos:
- La distribución binomial es aquella en la que se estudia la probabilidad de un número repetido de ensayos. Una distribución de probabilidad que proporciona el recuento de una serie de eventos independientes que ocurren aleatoriamente dentro de un período determinado, se denomina distribución de probabilidad.
- La distribución binomial es biparamétrica, yo.mi. aparece por dos parámetros N y P, mientras que la distribución de Poisson es uniparamétrica, i.mi. caracterizado por un solo parámetro m.
- Hay un número fijo de intentos en la distribución binomial. Por otro lado, hay un número ilimitado de pruebas en una distribución de Poisson.
- La probabilidad de éxito es constante en la distribución binomial, pero en la distribución de Poisson, hay un número extremadamente pequeño de posibilidades de éxito.
- En una distribución binomial, solo hay dos resultados posibles, yo.mi. éxito o fracaso. Por el contrario, hay un número ilimitado de resultados posibles en el caso de la distribución de Poisson.
- En la varianza de la media de distribución binomial, mientras que en la distribución de Poisson media = varianza.
Conclusión
Además de las diferencias anteriores, hay una serie de aspectos similares entre estas dos distribuciones I.mi. Ambos son la distribución de probabilidad teórica discreta. Además, sobre la base de los valores de los parámetros, ambos pueden ser unimodales o bimodales. Además, la distribución binomial puede ser aproximada mediante la distribución de Poisson, si el número de intentos (n) tiende al infinito y la probabilidad de éxito (P) tiende a 0 para que M = np.
- « Diferencia entre estadística y parámetro
- Diferencia entre el método de agrupación de interés y el método de compra »

