Diferencia entre correlación y regresión
- 2432
- 247
- Rubén Alarcón
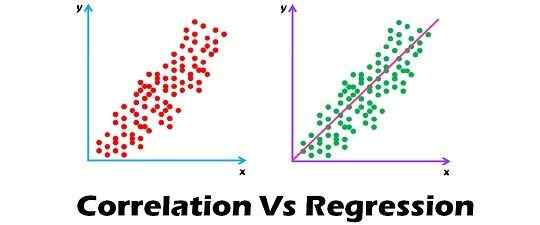
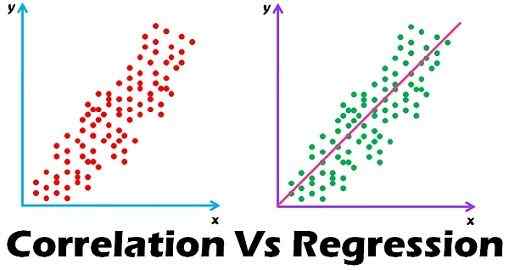 La correlación y la regresión son los dos análisis basados en la distribución multivariada. Una distribución multivariada se describe como una distribución de múltiples variables. Correlación se describe como el análisis que nos permite saber la asociación o la ausencia de la relación entre dos variables 'x' y 'y'. En el otro extremo, Regresión Análisis, predice el valor de la variable dependiente en función del valor conocido de la variable independiente, suponiendo que la relación matemática promedio entre dos o más variables.
La correlación y la regresión son los dos análisis basados en la distribución multivariada. Una distribución multivariada se describe como una distribución de múltiples variables. Correlación se describe como el análisis que nos permite saber la asociación o la ausencia de la relación entre dos variables 'x' y 'y'. En el otro extremo, Regresión Análisis, predice el valor de la variable dependiente en función del valor conocido de la variable independiente, suponiendo que la relación matemática promedio entre dos o más variables.
La diferencia entre correlación y regresión es una de las preguntas comúnmente hechas en las entrevistas. Además, muchas personas sufren ambigüedad al comprender estos dos. Por lo tanto, tome una lectura completa de este artículo para tener una comprensión clara de estos dos.
Contenido: correlación vs regresión
- Cuadro comparativo
- Definición
- Diferencias clave
- Video
- Conclusión
Cuadro comparativo
| Base para la comparación | Correlación | Regresión |
|---|---|---|
| Significado | La correlación es una medida estadística que determina la co-relación o la asociación de dos variables. | La regresión describe cómo una variable independiente está relacionada numéricamente con la variable dependiente. |
| Uso | Representar una relación lineal entre dos variables. | Para adaptarse a la mejor línea y estimar una variable sobre la base de otra variable. |
| Variables dependientes e independientes | Ninguna diferencia | Ambas variables son diferentes. |
| Indica | El coeficiente de correlación indica la medida en que dos variables se mueven juntas. | La regresión indica el impacto de un cambio de unidad en la variable conocida (x) en la variable estimada (y). |
| Objetivo | Para encontrar un valor numérico que exprese la relación entre variables. | Para estimar los valores de la variable aleatoria sobre la base de los valores de la variable fija. |
Definición de correlación
El término correlación es una combinación de dos palabras 'co' (juntas) y relación (conexión) entre dos cantidades. La correlación es cuando, en el momento del estudio de dos variables, se observa que un cambio unitario en una variable se representa por un cambio equivalente en otra variable, I.mi. directo o indirecto. O bien, se dice que las variables no están correlacionadas cuando el movimiento en una variable no equivale a ningún movimiento en otra variable en una dirección específica. Es una técnica estadística que representa la fuerza de la conexión entre pares de variables.
La correlación puede ser positiva o negativa. Cuando las dos variables se mueven en la misma dirección, yo.mi. Un aumento en una variable dará como resultado el aumento correspondiente en otra variable y viceversa, entonces las variables se consideran positivamente correlacionadas. Por ejemplo: ganancias e inversión.
Por el contrario, cuando las dos variables se mueven en diferentes direcciones, de tal manera que un aumento en una variable dará como resultado una disminución en otra variable y viceversa, esta situación se conoce como correlación negativa. Por ejemplo: Precio y demanda de un producto.
Las medidas de correlación se dan como bajo:
- El coeficiente de correlación de productos de productos de productos de Karl Pearson
- Coeficiente de correlación de rango de Spearman
- Diagrama de dispersión
- Coeficiente de desviaciones concurrentes
Definición de regresión
Una técnica estadística para estimar el cambio en la variable dependiente de la métrica debido al cambio en una o más variables independientes, basada en la relación matemática promedio entre dos o más variables se conoce como regresión. Desempeña un papel importante en muchas actividades humanas, ya que es una herramienta poderosa y flexible que solía pronosticar los eventos pasados, presentes o futuros sobre la base de eventos pasados o presentes. Por ejemplo: Sobre la base de registros pasados, se puede estimar la ganancia futura de una empresa.
En una regresión lineal simple, hay dos variables x e y, en las que y depende de x o digamos influenciado por x. Aquí se llama a una variable dependiente o de criterio y x es independiente o variable predictor. La línea de regresión de y en x se expresa como debajo:
y = a + bx
donde, a = constante,
b = coeficiente de regresión,
En esta ecuación, A y B son los dos parámetros de regresión.
Diferencias clave entre correlación y regresión
Los puntos dados a continuación explican la diferencia entre correlación y regresión en detalle:
- Una medida estadística que determina la co-relación o asociación de dos cantidades se conoce como correlación. La regresión describe cómo una variable independiente está relacionada numéricamente con la variable dependiente.
- La correlación se usa para representar la relación lineal entre dos variables. Por el contrario, la regresión se utiliza para adaptarse a la mejor línea y estimar una variable sobre la base de otra variable.
- En correlación, no hay diferencia entre las variables dependientes e independientes i.mi. La correlación entre x e y es similar a y y x. Por el contrario, la regresión de y en x es diferente de x en y.
- La correlación indica la fuerza de asociación entre las variables. A diferencia de, la regresión refleja el impacto del cambio de unidad en la variable independiente en la variable dependiente.
- La correlación tiene como objetivo encontrar un valor numérico que exprese la relación entre variables. A diferencia de la regresión cuyo objetivo es predecir los valores de la variable aleatoria sobre la base de los valores de la variable fija.
Video: correlación vs regresión
Conclusión
Con la discusión anterior, es evidente que hay una gran diferencia entre estos dos conceptos matemáticos, aunque estos dos se estudian juntos. La correlación se usa cuando el investigador quiere saber si las variables en estudio están correlacionadas o no, si es así, ¿cuál es la fuerza de su asociación?. El coeficiente de correlación de Pearson se considera la mejor medida de correlación. En el análisis de regresión, se establece una relación funcional entre dos variables para hacer proyecciones futuras en eventos.
- « Diferencia entre la empresa conjunta y la alianza estratégica
- Diferencia entre la evaluación formativa y sumativa »

