Diferencia entre eventos mutuamente excluyentes e independientes
- 1309
- 196
- Benjamín Urrutia
La probabilidad es un concepto matemático, que ahora se ha convertido en una disciplina completa y es una parte vital de las estadísticas. El experimento aleatorio en probabilidad es un rendimiento que genera un cierto resultado, basado únicamente en el azar. Los resultados de un experimento aleatorio se llaman evento. En probabilidad, existen varios tipos de eventos, como en simples, compuestos, mutuamente excluyentes, exhaustivos, independientes, dependientes, igualmente probables, etc. Cuando los eventos no pueden ocurrir al mismo tiempo, se llaman mutuamente excluyentes
Por otro lado, si cada evento no se ve afectado por otros eventos, se les llama eventos independientes. Tome una lectura completa del artículo presentado a continuación para tener una mejor comprensión de la diferencia entre eventos mutuamente excluyentes e independientes.
Contenido: evento mutuo exclusivo versus evento independiente
- Cuadro comparativo
- Definición
- Diferencias clave
- Conclusión
Cuadro comparativo
| Base para la comparación | Eventos mutuamente excluyentes | Eventos independientes |
|---|---|---|
| Significado | Se dice que dos eventos son mutuamente excluyentes, cuando su ocurrencia no es simultáneo. | Se dice que dos eventos son independientes, cuando la ocurrencia de un evento no puede controlar la ocurrencia de otros. |
| Influencia | La ocurrencia de un evento dará como resultado la no ocurrencia del otro. | La ocurrencia de un evento no tendrá influencia en la ocurrencia de la otra. |
| Fórmula matemática | P (A y B) = 0 | P (A y B) = P (A) P (B) |
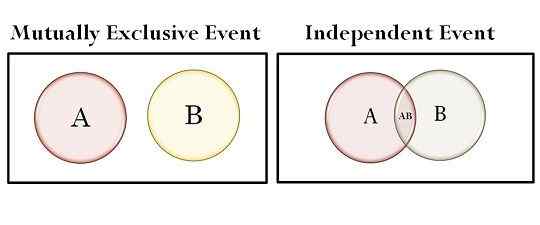
| Conjuntos en el diagrama de Venn | No se superpone | Superpuesto |
Definición de evento mutuamente excluyente
Los eventos mutuamente excluyentes son aquellos que no pueden ocurrir simultáneamente, yo.mi. donde la ocurrencia de un evento resulta en no ocurrencia del otro evento. Tales eventos no pueden ser ciertos al mismo tiempo. Por lo tanto, el suceso de un evento hace que el suceso de otro evento sea imposible. Estos también se conocen como eventos disjuntos.
Tomemos un ejemplo de lanzamiento de una moneda, donde el resultado sería la cabeza o la cola. Tanto la cabeza como la cola no pueden ocurrir simultáneamente. Tome otro ejemplo, suponga que si una empresa quiere comprar maquinaria, para la cual tiene dos opciones de máquina A y B. La máquina que es rentable y la productividad es mejor, se seleccionará. La aceptación de la máquina A dará como resultado automáticamente el rechazo de la máquina B y viceversa.
Definición de evento independiente
Como su nombre indica, los eventos independientes son los eventos, en los que la probabilidad de un evento no controla la probabilidad de ocurrencia del otro evento. El suceso o no hipappeding de tal evento no tiene absolutamente ningún efecto en el suceso o la falta de hippape de otro evento. El producto de sus probabilidades separadas es igual a la probabilidad de que ambos eventos ocurran.
Tomemos un ejemplo, supongamos que si una moneda se arroja dos veces, la cola en la primera oportunidad y la cola en la segunda, los eventos son independientes. Otro ejemplo para esto, supongamos que si un dado se enrolla dos veces, 5 en la primera oportunidad y 2 en el segundo, los eventos son independientes.
Diferencia clave entre eventos mutuamente excluyentes e independientes
Las diferencias significativas entre eventos mutuamente excluyentes e independientes se elaboran como bajo:
- Los eventos mutuamente excluyentes son esos eventos cuando su ocurrencia no es simultáneo. Cuando la ocurrencia de un evento no puede controlar la ocurrencia de otros, tales eventos se llaman evento independiente.
- En eventos mutuamente excluyentes, la ocurrencia de un evento dará como resultado la no ocurrencia del otro. Por el contrario, en eventos independientes, la ocurrencia de un evento no tendrá influencia en la ocurrencia de la otra.
- Los eventos mutuamente excluyentes se representan matemáticamente como P (A y B) = 0, mientras que los eventos independientes se representan como P (A y B) = P (A) P (B).
- En un diagrama de Venn, los conjuntos no se superponen entre sí, en el caso de eventos mutuamente excluyentes, mientras que si hablamos de eventos independientes, los sets se superponen.
Conclusión
Entonces, con la discusión anterior, está bastante claro que ambos eventos no son iguales. Además, hay un punto para recordar, y es si un evento es mutuamente excluyente, entonces no puede ser independiente y viceversa. Si dos eventos A y B son mutuamente excluyentes, entonces se pueden expresar como p (aub) = p (a)+p (b) mientras que si las mismas variables son independientes, entonces se pueden expresar como p (a∩b) = = P (A) P (B).