Diferencia entre la parábola y la hipérbola

Parábola vs hipérbola

La parábola y la hipérbola son dos secciones diferentes de un cono. Podemos lidiar con sus diferencias en una explicación matemática o lidiar con las diferencias de una manera muy simple que no solo los matemáticos, sino que todos pueden entender. Este artículo intentará explicar la diferencia entre ellos de una manera muy simple.
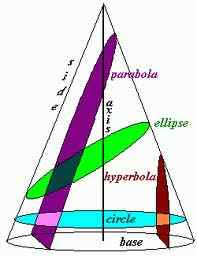
En primer lugar, cuando una figura sólida, que en este caso es un cono, es cortada por un plano, la sección que se obtiene se llama sección cónica. Las secciones cónicas podrían ser círculos, elipses, hipérbolas y paracolas dependiendo del ángulo de intersección entre el eje del cono y el plano. Tanto las parábolas como las hipérbolas son una curva abierta que significa que los brazos o ramas de las curvas continúan infinitando; No son curvas cerradas como un círculo o una elipse.

Parábola
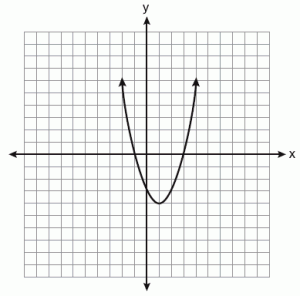
Una parábola es la curva obtenida cuando el avión se corta paralelo al lado del cono. En una parábola, una línea que pasa por el foco y perpendicular a la directriz se llama "eje de simetría."Cuando la parábola se cruza con el punto en el" eje de simetría ", se conoce como el" vértice."Todas las parábolas se forman de manera idéntica a medida que se cortan en un ángulo específico. Es un caracterizado por la excentricidad de "1."Esta es la razón por la que todos tienen la misma forma, pero pueden ser de diferentes tamaños.

La parábola viene dada por la ecuación y2 = x
Cuando un conjunto de puntos presentes en un plano es equidistante de la directriz, una línea recta dada, y es equidistante desde el foco, un punto dado que se fija, se llama parábola.
Las parábolas tienen muchas aplicaciones prácticas. Se utilizan para diseñar el camino de los misiles, los reflectores de los faros de los automóviles, los telescopios, los receptores de radar y los platos satelitales.

Hipérbola

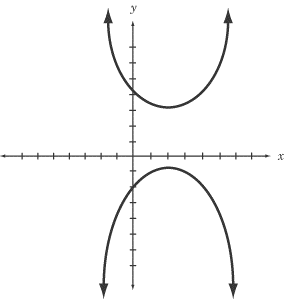
Hyperbola es la curva obtenida cuando el plano se corta casi paralelo al eje. Las hipérbolas no tienen forma idéntica, ya que hay muchos ángulos entre el eje y el plano. Los "vértices" son los puntos en los dos brazos que están más cerca; mientras que el segmento de línea que conecta los brazos se llama "eje principal."
En una parábola, los dos brazos de la curva, también llamados ramas, se vuelven paralelos entre sí. En una hipérbola, los dos brazos o curvas no se vuelven paralelas. El centro de un hipérbola es el punto medio del eje principal.

Hyperbola viene dada por la ecuación xy = 1

Cuando la diferencia de distancias entre un conjunto de puntos presentes en un plano a dos focos o puntos fijos es una constante positiva, se llama hipérbola.

Resumen:
Cuando un conjunto de puntos presentes en un plano es equidistante de la directriz, una línea recta dada, y es equidistante desde el foco, un punto dado que se fija, se llama parábola. Cuando la diferencia de distancias entre un conjunto de puntos presentes en un plano a dos focos o puntos fijos es una constante positiva, se llama hipérbola.
Todas las parápolas tienen la misma forma sin importar el tamaño; Todas las hipérbolas son de diferentes formas
La parábola viene dada por la ecuación y2 = x; La ecuación xy dada una hipérbola
En una parábola, los dos brazos se vuelven paralelos entre sí, mientras que en una hipérbola no.