Diferencia entre permutación y combinación

- 2683
- 550
- Adriana Preciado
 En matemáticas, es posible que hayas escuchado las nociones de permutación y combinación de un número final de veces, pero alguna vez has imaginado que estos dos son conceptos diferentes? La diferencia fundamental entre la permutación y la combinación es el orden de los objetos, en permutación El orden de los objetos es muy importante, yo.mi. La disposición debe estar en el orden estipulado del número de objetos, tomados solo algunos o todos a la vez.
En matemáticas, es posible que hayas escuchado las nociones de permutación y combinación de un número final de veces, pero alguna vez has imaginado que estos dos son conceptos diferentes? La diferencia fundamental entre la permutación y la combinación es el orden de los objetos, en permutación El orden de los objetos es muy importante, yo.mi. La disposición debe estar en el orden estipulado del número de objetos, tomados solo algunos o todos a la vez.
En contra de esto, en el caso de un combinación, La orden no importa en absoluto. No solo en matemáticas, sino también en la vida práctica, pasamos con estos dos conceptos regularmente. Aunque, nunca lo notamos. Entonces, lea el artículo cuidadosamente, para saber cómo estos dos conceptos son diferentes.
Contenido: permutación vs combinación
- Cuadro comparativo
- Definición
- Diferencias clave
- Ejemplo
- Conclusión
Cuadro comparativo
| Base para la comparación | Permutación | Combinación |
|---|---|---|
| Significado | La permutación se refiere a las diferentes formas de organizar un conjunto de objetos en un orden secuencial. | La combinación se refiere a varias formas de elegir elementos de un gran conjunto de objetos, de modo que su orden no importa. |
| Orden | Importante | Irrelevante |
| Denota | Acuerdo | Selección |
| Qué es? | Elementos ordenados | Conjuntos desordenados |
| Respuestas | ¿Cuántas disposiciones diferentes se pueden crear a partir de un conjunto dado de objetos?? | Cuántos grupos diferentes se pueden elegir entre un grupo más grande de objetos? |
| Derivación | Permutación múltiple de una sola combinación. | Combinación única de una sola permutación. |
Definición de permutación
Definimos la permutación como diferentes formas de organizar algunos o todos los miembros de un set en un orden específico. Implica toda la disposición o reordenamiento posible del conjunto dado, en orden distinguible.
Por ejemplo, Toda la permutación posible creada con letras x, y, z -
- Al tomar los tres a la vez, son Xyz, Xzy, YXZ, YZX, ZXY, Zyx.
- Tomando dos a la vez son XY, XZ, YX, YZ, ZX, ZY.
El número total de permutaciones posibles de n cosas, tomadas r a la vez, se pueden calcular como:
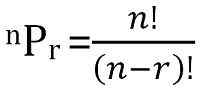
Definición de combinación
La combinación se define como las diferentes formas, de seleccionar un grupo, tomando algunos o todos los miembros de un conjunto, sin el siguiente orden.
Por ejemplo, Todas las combinaciones posibles elegidas con la letra m, n, o -
- Cuando se seleccionarán tres de tres letras, entonces la única combinación es MNO
- Cuando se seleccionarán dos de cada tres letras, entonces las posibles combinaciones son Mn, no, OM.
El número total de combinaciones posibles de n cosas, tomadas r a la vez se pueden calcular como:
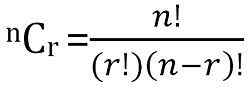
Diferencias clave entre permutación y combinación
Las diferencias entre la permutación y la combinación se dibujan claramente por los siguientes motivos:
- El término permutación se refiere a varias formas de organizar un conjunto de objetos en un orden secuencial. La combinación implica varias formas de elegir elementos de un gran grupo de objetos, de modo que su orden sea irrelevante.
- El principal punto distintivo entre estos dos conceptos matemáticos es el orden, la ubicación y la posición, I.mi. En las características de permutación mencionadas anteriormente, lo que no importa en el caso de la combinación.
- La permutación denota varias formas de organizar cosas, personas, dígitos, alfabetos, colores, etc. Por otro lado, la combinación indica diferentes formas de seleccionar elementos de menú, comida, ropa, temas, etc.
- La permutación no es más que una combinación ordenada, mientras que la combinación implica conjuntos no ordenados o emparejamiento de valores dentro de criterios específicos.
- Se pueden derivar muchas permutaciones de una sola combinación. Por el contrario, solo se puede obtener una sola combinación de una sola permutación.
- Permutación responde cuántos arreglos diferentes se pueden crear a partir de un conjunto de objetos dado? A diferencia de la combinación que explica cuántos grupos diferentes se pueden elegir de un grupo más grande de objetos?
Ejemplo
Supongamos que hay una situación en la que debe averiguar el número total de muestras posibles de dos de tres objetos A, B, C. En esta pregunta, en primer lugar, debe comprender si la pregunta está relacionada con la permutación o la combinación y la única forma de descubrir esto es verificar si el pedido es importante o no.
Si el pedido es significativo, entonces la pregunta está relacionada con la permutación, y las muestras posibles serán, AB, BA, BC, CB, AC, CA. Donde, AB es diferente de BA, BC es diferente de CB y AC es CA diferente.
Si el pedido es irrelevante, entonces la pregunta está relacionada con la combinación, y las posibles muestras serán AB, BC y CA.
Conclusión
Con la discusión anterior, está claro que la permutación y la combinación son términos diferentes, que se utilizan en matemáticas, estadísticas, investigación y nuestra vida cotidiana. Un punto para recordar, con respecto a estos dos conceptos es que, para un conjunto dado de objetos, la permutación siempre será más alta que su combinación.
- « Diferencia entre contabilidad y auditoría
- Diferencia entre la empresa conjunta y la alianza estratégica »

