Diferencia entre la media de la muestra y la media de la población

- 1450
- 211
- Carmen Arreola
 En estadística, la media aritmética es una de las medidas ideales de tendencia central. Para un conjunto dado de observaciones, la media aritmética se puede calcular agregando todas las observaciones y dividiendo el valor obtenido por el número de observaciones. Hay dos tipos de media, yo.mi. Media de muestra y media de población, que a menudo se usa en estadísticas y probabilidad. La media de la muestra se usa principalmente para estimar la media de la población cuando la media de la población no se conoce, ya que tienen el mismo valor esperado.
En estadística, la media aritmética es una de las medidas ideales de tendencia central. Para un conjunto dado de observaciones, la media aritmética se puede calcular agregando todas las observaciones y dividiendo el valor obtenido por el número de observaciones. Hay dos tipos de media, yo.mi. Media de muestra y media de población, que a menudo se usa en estadísticas y probabilidad. La media de la muestra se usa principalmente para estimar la media de la población cuando la media de la población no se conoce, ya que tienen el mismo valor esperado.
Muestra promedio implica la media de la muestra derivada de toda la población al azar. Población media no es más que el promedio de todo el grupo. Eche un vistazo a este artículo para conocer las diferencias entre la media de la muestra y la media de la población.
Contenido: Media de muestra vs Media de la población
- Cuadro comparativo
- Definición
- Diferencias clave
- Conclusión
Cuadro comparativo
| Base para la comparación | Muestra promedio | Población media |
|---|---|---|
| Significado | La media de la muestra es la media aritmética de los valores de muestra aleatorios extraídos de la población. | La media de la población representa la media real de toda la población. |
| Símbolo | x̄ (pronunciado como x bar) | μ (término griego MU) |
| Cálculo | Fácil | Difícil |
| Exactitud | Bajo | Alto |
| Desviación Estándar | Cuando se calcula usando la media de la muestra, se denota por (s) (s). | Cuando se calcula usando la media de la población, se denota por (σ). |
Definición de media de muestra
La media de la muestra es la media calculada a partir de un grupo de variables aleatorias, extraída de la población. Se considera un estimador eficiente e imparcial de la media de la población, lo que significa que el valor más esperado para la estadística de muestra es la estadística de población, independientemente del error de muestreo. La media de la muestra se calcula como debajo:
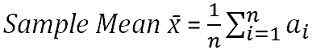 donde, n = tamaño de la muestra
donde, n = tamaño de la muestra
∑ = sumar
ai = Todas las observaciones
Definición de población media
En las estadísticas, la media de la población se define como el promedio de todos los elementos de la población. Es una media de la característica grupal, donde el grupo se refiere a elementos de la población como elementos, personas, etc. y la característica es el elemento de interés. Como la población es muy grande y no conocida, la media de la población es constante desconocida. Con la ayuda de la siguiente fórmula, se puede calcular la media de la población,
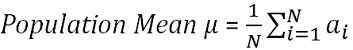 donde n = tamaño de la población
donde n = tamaño de la población
∑ = sumar
ai = Todas las observaciones
Diferencias clave entre la media de la muestra y la media de la población
Las diferencias significativas entre la media de la muestra y la media de la población se explican en detalle en los puntos que se detallan a continuación:
- La media aritmética de los valores de muestra aleatorios extraídos de la población se llama media de muestra. La media aritmética de toda la población se llama media población.
- La muestra está representada por x̄ (pronunciada como una barra x). Por otro lado, la media de la población se etiqueta como μ (término griego MU).
- Si bien el cálculo de la media de la muestra es fácil, ya que la lista de elementos proporcionados son solo pocos que consumen mucho menos tiempo. A diferencia de la media de la población, donde el cálculo es difícil, ya que hay muchos elementos en la población que toman mucho tiempo.
- La precisión de una media de población es relativamente mayor que la media de la muestra. La precisión de una media de muestra se puede mejorar aumentando el número de observaciones.
- Los elementos de la población están representados por 'n' en la población media. Por el contrario, 'n' en la media de la muestra representa el tamaño de la muestra.
- Cuando la desviación estándar se calcula utilizando la media de la muestra, se denota por letra 's'. Por el contrario, cuando la media de la población se usa en el cálculo de la desviación estándar, está representado por Sigma (σ).
Conclusión
El método de cálculo de ambos medios es el mismo, yo.mi. Suma de todas las observaciones divididas por el número de observaciones, pero hay una gran diferencia entre cómo están representados. Mientras que una media de muestra se escribe como x̄ o a veces m, la media de la población se etiqueta como μ. La media de la muestra es una variable aleatoria, mientras que la media de la población es una constante desconocida.

