Diferencia entre la asíntota horizontal y vertical

Antes de entrar en el tema de la asíntota horizontal y vertical, intentemos entender qué son exactamente las asíntotas y qué papel juegan en las matemáticas. En la geometría proyectiva, una asíntota es una línea recta que se acerca a una curva dada arbitrariamente pero no se encuentra a distancia finita. Geométricamente, una línea es una asíntota de una curva y = f (x), si la distancia entre la línea y un punto 'P' en la curva se acerca a cero, ya que X e Y tienden a infinito. Un gráfico puede tener una asíntota paralela a cada eje. En realidad, una asíntota es algo que no está allí físicamente: es más como la fantasía.

Una asíntota ayuda a determinar las acciones o las formas de las cosas, pero no es realmente una parte del gráfico. Es simplemente una línea imaginaria que te ayuda a graficar una función racional. A medida que la curva se acerca hacia una asíntota, se acerca cada vez más a la asíntota, pero en realidad nunca la toca. Por lo tanto, la asíntota ayuda a determinar hacia dónde puede o no ir la gráfica de la función. Dicho esto, hay tres tipos de asíntotas: asíntotas verticales, horizontales y oblicuas. Pero solo discutiremos las asíntotas verticales y las asíntotas horizontales, y veremos cómo descubrir cuál es lo que realmente.

¿Qué es la asíntota horizontal??

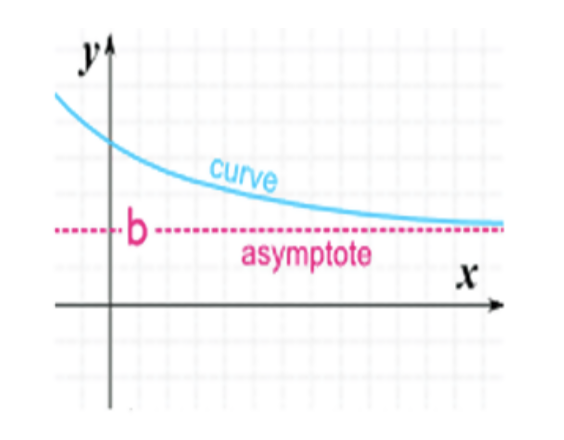
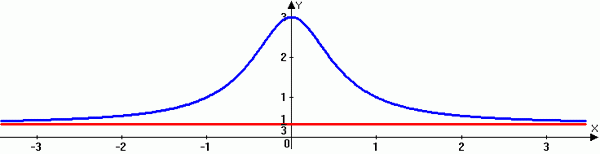
Una asíntota horizontal es un valor constante en un gráfico que se acerca una función pero en realidad no alcanza. Indica lo que realmente le sucede a la curva a medida que los valores X se vuelven muy grandes o muy pequeños. En los ejemplos gráficos anteriores, la curva se acerca a un valor constante B, pero nunca alcanza, y = 0.

La línea y = b es una asíntota horizontal de la gráfica de 'f' if f (x) -> b como x -> ∞ o x -> -∞

Para encontrar una asíntota horizontal de una función racional, se debe considerar el grado de los polinomios en el numerador y el denominador.

• Si el denominador tiene la potencia variable más alta en la ecuación de funciones, la asíntota horizontal es automáticamente el eje x o y = 0.
• Si tanto el numerador como el denominador tienen el mismo grado, tome los coeficientes principales de esos términos con la mayor potencia y haga una fracción de ellos para encontrar la asíntota horizontal
• Si el numerador tiene la potencia variable más alta en la ecuación de la función, la función no tiene asíntota horizontal; El gráfico probablemente tendrá una asíntota oblicua.

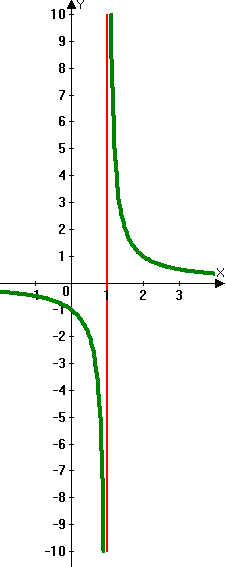
¿Qué es la asíntota vertical??

Como el denominador de una fracción nunca puede ser cero, tener la variable en la parte inferior si una fracción puede ser un problema. Algún valor de dominio de 'x' hace que el denominador sea cero y la función saltará sobre este valor en el gráfico, creando una asíntota vertical. Son líneas verticales dibujadas a la ligera o con guiones para demostrar que no son parte del gráfico.

Si el número real 'a' es un cero del denominador q (x), entonces la gráfica de f (x) = p (x)/q (x), donde p (x) y q (x) no tienen comunes factores, tiene la asíntota vertical, x = a.

Diferencia entre la asíntota horizontal y vertical

Definición

- Una asíntota horizontal es un valor constante en un gráfico que se acerca una función pero en realidad no alcanza. Indica lo que realmente le sucede a la curva a medida que los valores X se vuelven muy grandes o muy pequeños. Las asíntotas verticales, por otro lado, son líneas verticales invisibles que corresponden al cero en el denominador de una fracción racional. Son líneas verticales dibujadas a la ligera o con guiones para demostrar que no son parte del gráfico.

Cálculo

- Para determinar una asíntota horizontal de una función racional, se debe considerar el grado de los polinomios en el numerador y el denominador. Si el denominador tiene la potencia variable más alta en la ecuación de funciones, la asíntota horizontal es automáticamente el eje x o y = 0. Si tanto el numerador como el denominador tienen el mismo grado, entonces haga una fracción de sus coeficientes para determinar la ecuación de asíntota horizontal. Para determinar las asíntotas verticales de una función racional, establezca el denominador de la fracción igual a cero.

Ejemplo

- Descubra las asíntotas de la función

Y = 3x²+9x-21 ∕ x²-25

Para encontrar las asíntotas verticales, establezca el denominador de la fracción igual a cero.

X²-25 = 0

(x-5) (x+5) = 0

x = 5 y x = - 5

Estos dos números son los dos valores que no se pueden incluir en el dominio, por lo que las ecuaciones son asíntotas verticales. Entonces, las dos asíntotas verticales son, x = 5 y x = - 5.

Ahora, para determinar la asíntota horizontal, mire la ecuación original. Aquí, la potencia variable más alta es 2. Como tanto el numerador como el denominador tienen el mismo grado de potencia, haga una fracción de sus coeficientes:

y = 3x²/X²

y = 3/1

y = 3

Entonces, la ecuación de la asíntota horizontal es, y = 3.

Asíntota horizontal vs. Asíntota vertical: tabla de comparación

Resumen de asíntota horizontal vs. Asíntota vertical

Una asíntota ayuda a determinar las acciones o las formas de las cosas, pero no es realmente una parte del gráfico. Las asíntotas verticales marcan los lugares donde la función no tiene dominio. Usted resuelve para la ecuación de las asíntotas verticales estableciendo el denominador de la fracción igual a cero. Las asíntotas horizontales, por otro lado, indican qué sucede con la curva a medida que los valores X se vuelven muy grandes o muy pequeños. Para encontrar una asíntota horizontal, debe considerar el grado de los polinomios en el numerador y el denominador.