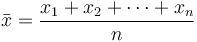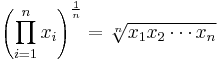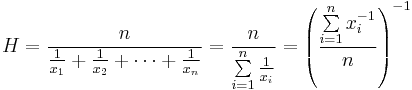Medio VS. Mediana

- 1728
- 436
- Juan Carlos Rodrígez
Significar (o promedio) y mediana son términos estadísticos que tienen un papel algo similar en términos de comprender el tendencia central de un conjunto de puntajes estadísticos. Si bien un promedio ha sido tradicionalmente una medida popular de un punto medio en una muestra, tiene la desventaja de verse afectado por que cualquier valor sea demasiado alto o demasiado bajo en comparación con el resto de la muestra. Es por eso que una mediana a veces se toma como una mejor medida de un punto medio.
Cuadro comparativo
| Significar | Mediana | |
|---|---|---|
| Definición | La media es el promedio aritmético de un conjunto de números o distribución. Es la medida más utilizada de la tendencia central de un conjunto de números. | La mediana se describe como el valor numérico que separa la mitad más alta de una muestra, una población o una distribución de probabilidad, de la mitad inferior. |
| Aplicabilidad | La media se usa para distribuciones normales. | La mediana se usa generalmente para distribuciones sesgadas. |
| Relevancia para el conjunto de datos | La media no es una herramienta robusta, ya que está en gran medida influenciada por valores atípicos. | La mediana es más adecuada para que las distribuciones sesgadas se deriven a la tendencia central, ya que es mucho más robusta y sensata. |
| Como calcular | Se calcula una media sumando todos los valores y dividiendo esa puntuación por el número de valores. | La mediana es el número que se encuentra en el medio exacto del conjunto de valores. Se puede calcular una mediana enumerando todos los números en orden ascendente y luego localizando el número en el centro de esa distribución. |
Definiciones de media y mediana
En matemáticas y estadísticas, la media o la significado aritmetico de una lista de números es la suma de la lista completa dividida por el número de elementos en la lista. Al observar las distribuciones simétricas, la media es probablemente la mejor medida para llegar a la tendencia central. En teoría y estadística de probabilidad, un mediana es ese número que separa la mitad más alta de una muestra, una población o una distribución de probabilidad, de la mitad inferior.
Como calcular
El Significar o el promedio es probablemente el método más utilizado para describir la tendencia central. Se calcula una media sumando todos los valores y dividiendo esa puntuación por el número de valores. El significado aritmetico de una muestra 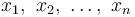 es la suma los valores muestreados divididos por el número de elementos en la muestra:
es la suma los valores muestreados divididos por el número de elementos en la muestra:
El Mediana es el número encontrado en el medio exacto del conjunto de valores. Se puede calcular una mediana enumerando todos los números en orden ascendente y luego localizando el número en el centro de esa distribución. Esto es aplicable a una lista de números impares; En caso de un número par de observaciones, no hay un valor medio único, por lo que es una práctica habitual tomar la media de los dos valores medios.
Ejemplo
Digamos que hay nueve estudiantes en una clase con los siguientes puntajes en una prueba: 2, 4, 5, 7, 8, 10, 12, 13, 83. En este caso el puntaje promedio (o el significar) es la suma de todos los puntajes divididos por nueve. Esto funciona a 144/9 = 16. Tenga en cuenta que a pesar de que 16 es el promedio aritmético, se distorsiona por la puntuación inusualmente alta de 83 en comparación con otros puntajes. Casi todos los puntajes de los estudiantes son abajo la media. Por lo tanto, en este caso la media no es un buen representante del tendencia central de esta muestra.
El mediana, Por otro lado, es el valor que es tal que la mitad de los puntajes están por encima y la mitad de los puntajes a continuación. Entonces, en este ejemplo, la mediana es 8. Hay cuatro puntajes debajo y cuatro por encima del valor 8. Entonces 8 representa el punto medio o la tendencia central de la muestra.
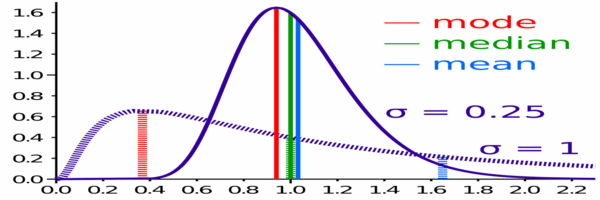 Comparación de la media, mediana y modo de dos distribuciones log-normales con una asimetría diferente.
Comparación de la media, mediana y modo de dos distribuciones log-normales con una asimetría diferente. Desventajas de los medios aritméticos y medianos
La media no es una herramienta estadística robusta, ya que no se puede aplicar a todas las distribuciones, pero es fácilmente la herramienta estadística más utilizada para derivar la tendencia central. La razón por la que no se puede aplicar la media a todas las distribuciones es porque se ve afectado indebidamente por valores en la muestra que son demasiado pequeños para demasiado grandes.
La desventaja de la mediana es que es difícil manejar teóricamente. No hay una fórmula matemática fácil para calcular la mediana.
Otros tipos de medios
Hay muchas formas de determinar la tendencia central o promedio de un conjunto de valores. La media discutida anteriormente es técnicamente la media aritmética, y es la estadística más utilizada para el promedio. Hay otros tipos de medios:
Significado geometrico
La media geométrica se define como la nortela raíz del producto de norte Números, yo.mi., Para un conjunto de números X1,X2,… ,Xnorte, La media geométrica se define como
Los medios geométricos son mejores que los medios aritméticos para describir el crecimiento proporcional. Por ejemplo, una buena aplicación para la media geométrica es calcular la tasa de crecimiento anual compuesta (CAGR).
Significado armonico
La media armónica es el recíproco de la media aritmética de los recíprocos. La media armónica H de los números reales positivos X1,X2,… ,Xnorte es
Una buena aplicación para medios armónicos es cuando se promedia múltiplos. Para Exampe, es mejor usar una media armónica ponderada al calcular la relación promedio de ganancias de precios (P/E). Si las relaciones P/E se promedian utilizando una media aritmética ponderada, los puntos de datos altos obtienen pesos excesivamente mayores que los puntos de datos bajos.
Medios pitagóricos
La media aritmética, la media geométrica y la media armónica juntas forman un conjunto de medios llamados medios pitagóricos. Para cualquier conjunto de números, la media armónica es siempre la más pequeña de todos los medios pitagóricos, y la media aritmética es siempre la más grande de los 3 medios. i.mi. Media armónica ≤ media geométrica ≤ media aritmética.
Otros significados de las palabras
Significar puede usarse como una figura del habla y tiene una referencia literaria. También se usa para implicar pobre o no ser genial. Mediana, En una referencia geométrica, hay una línea recta que pasa desde un punto en el triángulo hasta el centro del lado opuesto.